TEORIAS E FILOSOFIAS DE GRACELI 281
- Gerar link
- X
- Outros aplicativos
RELATIVIDADE GRACELI SOBRE Difração de elétrons NO SDCTIE GRACELI
sexta-feira, 15 de novembro de 2019
Difração de elétrons[editar | editar código-fonte]

Simulação numérica feita a partir da equação de Schrödinger. Na animação, um pacote de ondas (modelando uma partícula quântica livre) incide sobre uma fenda dupla. Note que o padrão formado após a passagem pela fenda, coincide com o já conhecido resultado do padrão de interferência.
A profunda contradição entre a teoria e a prática experimental atesta a construção de uma teoria aplicável aos fenômenos atômicos. Os fenômenos que ocorrem com partículas de massa muito pequena e em regiões muito pequenas do espaço, exige um caminho especial onde as leis e as idéias clássicas fundamentais devem ser reordenadas.
O ponto de partida para esclarecer esta troca de mentalidade para a dedução das leis que regem a física atômica, foi o fenômeno observado e chamado de difração de elétrons.
Na verdade, este fenômeno foi descoberto depois de criada a teoria da mecânica quântica.
Se fizermos passar um feixe homogêneo de elétrons através de um prisma, o que se observa é uma figura constituída de máximos e mínimos de intensidade variável que se sucedem entre si, análoga à figura que se obtêm na difração das ondas eletromagnéticas.
x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Simulação numérica feita a partir da equação de Schrödinger. Na animação, um pacote de ondas (modelando uma partícula quântica livre) incide sobre uma fenda dupla. Note que o padrão formado após a passagem pela fenda, coincide com o já conhecido resultado do padrão de interferência.
Difração de raios X é um fenômeno no qual os átomos de um cristal, em virtude de seu espaçamento uniforme, causam um padrão de interferência das ondas presentes em um feixe incidente de raios X. É uma técnica usada para determinar a estrutura atômica e molecular de um cristal, na qual os átomos cristalinos fazem com que um feixe de raios X incidentes difrate em muitas direções específicas. Medindo os ângulos e as intensidades dos feixes difratados, um cristalógrafo pode produzir uma imagem tridimensional da densidade de elétrons dentro do cristal. A partir desta densidade de elétrons, as posições médias dos átomos no cristal podem ser determinadas, bem como suas ligações químicas, sua desordem e várias outras informações[1]. O material analisado é finamente triturado, homogeneizado e a composição média em massa é determinada (difração de raios X em pó)[2].
História[editar | editar código-fonte]
Em 1933, o químico inglês Patrick Linstead lançou-se no estudo da estrutura atômica da ftalocianina de cobre. Para isso, ele utilizou a difração de raios X - essa técnica não é microscopia, pois fornece uma imagem “indireta” da molécula. Como seu nome indica, ela se baseia no fenômeno de difração – o mesmo que tanto instiga a microscopia. Raios X enviados sobre um cristal da amostra a ser analisada, fornecem uma imagem geométrica, de acordo com as distâncias interatômicas, o que permite remontar à estrutura do cristal. Num cristal de moléculas, bilhões de moléculas idênticas são empilhadas. Mantidas no lugar por suas vizinhas, elas pouco se mexem: este é um ponto crucial para realizar a imagem. Quando o cristal é suficientemente fino, a luz visível consegue atravessá-lo. Entretanto, seu comprimento de onda (de 400 a 800 nanometros) é grande demais para transmitir uma informação: é um pouco como se tentássemos agarrar uma avelã com uma retroescavadeira. É necessário utilizar comprimentos de onda bem menores. Os raios X convêm perfeitamente: têm comprimentos de onda equivalentes às distancias entre os átomos num cristal, ou seja, alguns nanômetros, até menos. É graças a eles, para citar apenas um dos primeiros exemplos históricos, que conhecemos a estrutura do cloreto de sódio, ou sal de cozinha: malhas quadradas de 0,4 nanometro de lado, cujos topos são ocupados por íons cloro e sódio. Patrick Linstead entregou seus cristais de ftalocianina de cobre a um jovem pesquisador, John Robertson, que efetuou longos cálculos para determinar a organização das moléculas no cristal (Figura 2) e para compreender a organização da própria molécula: trata-se de um quadrado de 1,3 nanometro de lado[3].
Um dos métodos importantes para caracterizar o arranjo de moléculas em um cristal é o método da difração de raios X. Ele fornece a posição relativa dos átomos que constituem o cristal e, consequentemente, o arranjo espacial entre as moléculas no mesmo. É claro que as estruturas que o método fornece será aquela que a substância toma na forma sólida cristalina. Em solução, quando a molécula estiver solvatada, a estrutura poderá não ser mais exatamente a mesma.
A difração de raios X tem tido um êxito particular – e porque não dizer espetacular – na determinação da estrutura de moléculas complexas e muito complexas, que valeram aos cientistas que nela trabalharam vários prêmios Nobel. Entre as complexas, pode-se citar a estrutura da vitamina B12 e da penicilina, determinadas por Dorothy Hodgkin (Prêmio Nobel de Química em 1964). Entre as moléculas muito complexas, estão proteínas – as estruturas da mioglobina (1958) e da hemoglobina (1960) foram determinadas por Kendrew e Perutz, respectivamente, o que lhes valeu o prêmio Nobel de Química em 1962 – e a do Ácido Desoxiribonucleico – DNA – talvez a de conseqüências mais profundas na Biologia e mesmo na ciência moderna – por Watson e Cricks em 1953 (Prêmio Nobel de Medicina em 1962)[4].
A descoberta[editar | editar código-fonte]
O século XIX ficou marcado por grandes descobertas que revolucionaram a ciência. Um dos experimentos que abriu as portas para diversos estudos foi o que envolvia a passagem de descargas elétricas através de um tubo de vidro contendo gases rarefeitos, conectado a uma bomba de vácuo (Figura 3). Com a saída do gás e a diminuição da pressão dentro do tubo, um fenômeno é observado na parte oposta ao catodo, essa começa a emitir uma incandescência esverdeada. Willian Crookes, em 1875, concluiu que essa luminescência era algum tipo de radiação que partia do terminal negativo indo em direção ao terminal positivo, denominado de raios catódicos.
 Em 1894, Wilhelm Conrad Röntgen (Figura 4) se interessou pelo trabalho publicado pelo físico Phillip Lenard, sobre os raios catódicos. Ele então iniciou uma série de experimentos com o objetivo de estudar tais radiações e foi em 8 de novembro de 1895, em mais um dia de trabalho, que ele observou que a folha de papel tratada com platinocianeto de bário, deixada próxima ao tudo de raios catódicos, brilhava no escuro, emitindo uma luz.[5] O tubo foi coberto com uma cartolina preta e mesmo assim o papel brilhava, colocou diversos objetos entre o tubo e o papel e os mesmos pareciam ser transparentes. Foi então nesse momento que ele viu os ossos de sua mão na tela. Após ter registrado suas observações em chapas fotográficas, fez então o anuncio a comunidade, dizendo que pela primeira vez poderia ver dentro do corpo humano sem abri-lo. Através do então denominado por ele, raios X.
Em 1894, Wilhelm Conrad Röntgen (Figura 4) se interessou pelo trabalho publicado pelo físico Phillip Lenard, sobre os raios catódicos. Ele então iniciou uma série de experimentos com o objetivo de estudar tais radiações e foi em 8 de novembro de 1895, em mais um dia de trabalho, que ele observou que a folha de papel tratada com platinocianeto de bário, deixada próxima ao tudo de raios catódicos, brilhava no escuro, emitindo uma luz.[5] O tubo foi coberto com uma cartolina preta e mesmo assim o papel brilhava, colocou diversos objetos entre o tubo e o papel e os mesmos pareciam ser transparentes. Foi então nesse momento que ele viu os ossos de sua mão na tela. Após ter registrado suas observações em chapas fotográficas, fez então o anuncio a comunidade, dizendo que pela primeira vez poderia ver dentro do corpo humano sem abri-lo. Através do então denominado por ele, raios X.Em 1912, o físico alemão Von Laue sugeriu que, se os átomos apresentam uma estrutura cristalina (átomos organizados de forma a apresentarem periodicidade ao longo do espaço) e se os raios X eram ondas eletromagnéticas com comprimento de onda menor que os espaços interatômicos, então os núcleos atômicos que concentram a massa dos átomos poderiam difratar os raios X, formando franjas de difração. Quando Laue fez passar um feixe de raios X por uma amostra monocristalina e pôs um filme fotográfico após a amostra, o resultado foi que, após revelar o filme, ele apresentava pontos sensibilizados pelos raios X difratados.
As experiências de Laue despertaram grande interesse nos físicos ingleses, W. H. Bragg e seu filho W. L. Bragg, que formularam, ainda em 1913, uma equação extremamente simples para prever os ângulos onde seriam encontrados os picos de intensidade máxima de difração. Assim, conhecendo-se as distâncias interatômicas, poderiam ser resolvidas os problemas envolvidos na determinação da estrutura cristalina. Dessa forma, os Bragg determinaram sua primeira estrutura, a do NaCl (Figura 5). Transformando a difração de raios X na primeira ferramenta eficiente para determinar a estrutura atômica dos materiais, fazendo com que a técnica obtivesse rapidamente grande popularidade entre os institutos de pesquisa.
Entre as décadas de 1920 e 1930, a literatura foi inundada por estruturas cristalinas determinadas por difração de raios X. Todo mineralogista ou cristalógrafo da época tinha por obrigação determinar a estrutura cristalina de algum composto, mineral ou metal. A difração de raios X também provocou surpresa ao demonstrar a estrutura amorfa do vidro, e também foi a principal ferramenta usada por Watson e Crick, em 1953, para propor a estrutura em dupla hélice do DNA[6].
Produção e medição de raios-X.[editar | editar código-fonte]
A fonte de raios-X de laboratório consiste em um tubo de vácuo no qual os elétrons são emitidos a partir de um filamento de tungstênio aquecido e acelerado por um potencial elétrico (tipicamente várias dezenas de kilovolts) para impactar um alvo de metal arrefecido a água. Quando os elétrons internos do alvo são ejetados e os exteriores caem para tomar seu lugar, os raios X são emitidos. Alguns têm uma distribuição contínua de comprimentos de onda entre cerca de 0,5 Å e 5 Å ("radiação branca") e alguns têm comprimentos de onda característicos dos níveis eletrônicos no alvo. Para a maioria das experiências, uma única radiação característica é selecionada usando um filtro ou monocromador[7]. Em relação aos detectores, no passado a maioria dos trabalhos de raio-X foi feito com filme, agora são usados detectores eletrônicos. Pode utilizar-se um único ponto (por exemplo Geiger Muller, contador de cintilação ou proporcional), um detector de linha (1D) ou um detector de área (2D).
Fundamentação teórica[editar | editar código-fonte]
O fenômeno de difração de raios X por cristais resulta de um processo de espalhamento no qual os raios X são dispersos pelos elétrons dos átomos sem alteração no comprimento de onda. Um feixe difratado é produzido por tal dispersão somente quando certas condições geométricas são satisfeitas, o que pode ser expresso em qualquer uma de duas formas, a equação de Bragg, ou a de Laue. O padrão de difração resultante de um cristal, que compreende tanto as posições como as intensidades dos efeitos de difração, é uma propriedade física fundamental da substância, servindo não apenas para sua rápida identificação, mas também para a elucidação completa de sua estrutura. A análise das posições do efeito de difração leva imediatamente a um conhecimento do tamanho, forma e orientação da célula unitária. Para localizar as posições dos átomos individuais na célula, as intensidades devem ser medidas e analisadas. O mais importante para relacionar as posições dos átomos com as intensidades de difração é a equação do fator de estrutura[8].
A dispersão[editar | editar código-fonte]
A dispersão de raios X é determinada pela densidade de elétrons dentro do cristal. Como a energia de um raio X é muito maior que a de um elétron de valência, a dispersão pode ser modelada como a dispersão de Thomson, a interação de um raio eletromagnético com um elétron livre. Este modelo é geralmente adotado para descrever a polarização da radiação dispersa, conforme descrito na derivação matemática abaixo[9].
A intensidade da dispersão de Thomson para uma partícula com massa  e carga
e carga  é:
é:
 e carga
e carga  é:
é:
x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Assim, os núcleos atômicos, que são muito mais pesados do que um elétron, contribuem de forma negligenciável para os raios-X dispersos.
Dispersão de raios X por elétrons e átomos[editar | editar código-fonte]
Os raios X são ondas eletromagnéticas e, como tal, são constituídos de um pacote de energia formado por um campo elétrico oscilante, denominado de fóton. Um fóton aos se interagir com um elétron é absorvido, elevando o elétron a um estado excitado, e ele ao voltar a seu estado natural, se torna uma fonte de ondas eletromagnética com mesma frequência e comprimento de onda do fóton absorvido (apenas em caso de espalhamentos). Dessa interação surge assim uma nova frente de onda esférica de raios X, com o elétron como sua origem, derivando sua energia do feixe incidente. Por este processo diz-se que o elétron dispersa o feixe original[8]. Um átomo é constituído por um núcleo carregado positivamente rodeado por uma nuvem de elétrons, um para cada incremento de carga nuclear, sendo o número igual ao número atômico do elemento em questão. As ondas dispersas dos diversos elétrons num átomo combinam-se, de modo que o efeito de dispersão de um átomo pode ser considerado como essencialmente o de uma fonte pontual de raios X dispersos. A intensidade da dispersão é, obviamente, dependente do número de elétrons no átomo, mas porque os elétrons estão distribuídos ao longo do volume do átomo em vez de concentrados em um ponto, a intensidade varia com a direção. No entanto, no presente caso, no tratamento da geometria da difração, o átomo é considerado uma fonte de dispersão pontual.
Dispersão por uma linha de átomos espaçados regularmente[editar | editar código-fonte]
Fenômenos de interferência com ondas de água e luz são bem conhecidos. De uma forma semelhante, podem surgir interferências construtivas e destrutivas entre as ondas de raios X dispersas dos átomos. Suponha que um feixe de raios X encontre uma fileira de átomos espaçados regularmente, como na Fig. 6. As frentes de onda paralelas fazem com que cada átomo se torne uma fonte de um conjunto de ondas esféricas dispersas da mesma freqüência e comprimento de onda. Na Fig. 6 consideramos a sucessão de cristas de onda e depressões de dois átomos vizinhos em algum instante no tempo. É necessário apenas considerar a dispersão em torno de um par de átomos vizinhos, pois a distância interatômica e o comprimento de onda dos raios X determinam a geometria dos efeitos de difração. A dispersão de átomos mais distantes na fileira contribui apenas (para os mesmos sentidos angulares) para os feixes dispersos representados na Fig. 6. Todos os pontos de interseção dos dois conjuntos de arcos concêntricos são pontos em que as cristas das ondas de ambos os átomos coincidem e suas amplitudes adicionam, levando a interferência construtiva e um máximo de difração. Em pontos entre as interseções, as ondas estão mais ou menos fora de fase e levam a vários graus de interferência destrutiva ou extinção.
Uma direção óbvia de reforço é aquela perpendicular à frente de onda original. Aqui a diferença de crista de onda entre as ondas dispersas dos dois átomos é zero, e dá origem ao feixe difratado de ordem zero. À direita do feixe de ordem zero é uma direção proeminente de interseções de crista caracterizada por uma crista de onda ou diferença de fase. Este é o feixe de difração de primeira ordem. Da mesma forma, mais à direita, segunda ordem, terceira ordem, e assim por diante para a ordem n, vigas difratadas representam 2, 3, 4,. . , N diferenças na fase da onda (comprimento de onda) na fase entre as ondas dos átomos vizinhos. As ordens negativas correspondentes de difração (menos primeira ordem, menos segunda ordem, etc.) surgem no lado oposto da direção do feixe de ordem zero. Embora a Fig. 6 represente o caso especial de um feixe incidindo em ângulos retos em uma linha de átomos, o caso geral de um feixe fazendo qualquer ângulo com a fileira é inteiramente análogo[8].
Condições para difração por uma malha linear de átomos[editar | editar código-fonte]
Uma linha reta de átomos regularmente espaçados constitui uma rede linear. Considere que um feixe paralelo de raios X encontra-se com uma tal linha de átomos com um ângulo  (Fig. 7),
(Fig. 7),  sendo o espaçamento constante entre os átomos. Todos os átomos da linha atuam como centros para séries de ondas dispersas, e o reforço que conduz a vigas difratadas de zero, primeiro, segundo e maior ocorre em certas direções. Suponha que uma dessas direções de interferência construtiva faça um ângulo com o eixo da linha. Então, uma vez que os raios X espalhados em D devem estar em fase com aqueles espalhados em G, os caminhos DE e FG devem diferir por um número inteiro de comprimentos de onda. Isso é:
sendo o espaçamento constante entre os átomos. Todos os átomos da linha atuam como centros para séries de ondas dispersas, e o reforço que conduz a vigas difratadas de zero, primeiro, segundo e maior ocorre em certas direções. Suponha que uma dessas direções de interferência construtiva faça um ângulo com o eixo da linha. Então, uma vez que os raios X espalhados em D devem estar em fase com aqueles espalhados em G, os caminhos DE e FG devem diferir por um número inteiro de comprimentos de onda. Isso é:
 (Fig. 7),
(Fig. 7),  sendo o espaçamento constante entre os átomos. Todos os átomos da linha atuam como centros para séries de ondas dispersas, e o reforço que conduz a vigas difratadas de zero, primeiro, segundo e maior ocorre em certas direções. Suponha que uma dessas direções de interferência construtiva faça um ângulo com o eixo da linha. Então, uma vez que os raios X espalhados em D devem estar em fase com aqueles espalhados em G, os caminhos DE e FG devem diferir por um número inteiro de comprimentos de onda. Isso é:
sendo o espaçamento constante entre os átomos. Todos os átomos da linha atuam como centros para séries de ondas dispersas, e o reforço que conduz a vigas difratadas de zero, primeiro, segundo e maior ocorre em certas direções. Suponha que uma dessas direções de interferência construtiva faça um ângulo com o eixo da linha. Então, uma vez que os raios X espalhados em D devem estar em fase com aqueles espalhados em G, os caminhos DE e FG devem diferir por um número inteiro de comprimentos de onda. Isso é: (equação 1)
(equação 1)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Onde  é um número inteiro, e
é um número inteiro, e  é o comprimento de onda do feixe de raio-x. De Trigonometria simples.
é o comprimento de onda do feixe de raio-x. De Trigonometria simples.
 é um número inteiro, e
é um número inteiro, e  é o comprimento de onda do feixe de raio-x. De Trigonometria simples.
é o comprimento de onda do feixe de raio-x. De Trigonometria simples. , e
, e  (equação 2)
(equação 2)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Daí a diferença de trajetória é:
 (equação 3)
(equação 3)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
E a equação 3 é a condição a ser satisfeita pelas várias ordens discretas de feixes difratados a partir dessa fileira de rede. A direção de qualquer ordem dada de feixe difratado é obtida pela resolução de  e substituindo o valor apropriado de
e substituindo o valor apropriado de  ,
,
 e substituindo o valor apropriado de
e substituindo o valor apropriado de  ,
, (equação 4)
(equação 4)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Obviamente, o feixe incidente poderia ter encontrado a linha de rede no ângulo  ao invadir a fileira de qualquer direção que seja um gerador de um cone concêntrico com a fileira e do ângulo
ao invadir a fileira de qualquer direção que seja um gerador de um cone concêntrico com a fileira e do ângulo  do semi ápice (Figura 8) . O local de todos os feixes de ordem zero é, então, um cone idêntico com um ápice comum no ponto de intersecção do feixe com a fileira de átomos; E os feixes incidentes e de ordem zero são geradores diametralmente opostos dos dois cones. As direções que satisfazem a equação 4 para as outras ordens difratadas do feixe encontram-se em outros cones com o mesmo ápice comum e os ângulos de semi-ápice apropriados
do semi ápice (Figura 8) . O local de todos os feixes de ordem zero é, então, um cone idêntico com um ápice comum no ponto de intersecção do feixe com a fileira de átomos; E os feixes incidentes e de ordem zero são geradores diametralmente opostos dos dois cones. As direções que satisfazem a equação 4 para as outras ordens difratadas do feixe encontram-se em outros cones com o mesmo ápice comum e os ângulos de semi-ápice apropriados  (Fig. 8). Note-se que
(Fig. 8). Note-se que  =
=  .[8]
.[8]
 ao invadir a fileira de qualquer direção que seja um gerador de um cone concêntrico com a fileira e do ângulo
ao invadir a fileira de qualquer direção que seja um gerador de um cone concêntrico com a fileira e do ângulo  do semi ápice (Figura 8) . O local de todos os feixes de ordem zero é, então, um cone idêntico com um ápice comum no ponto de intersecção do feixe com a fileira de átomos; E os feixes incidentes e de ordem zero são geradores diametralmente opostos dos dois cones. As direções que satisfazem a equação 4 para as outras ordens difratadas do feixe encontram-se em outros cones com o mesmo ápice comum e os ângulos de semi-ápice apropriados
do semi ápice (Figura 8) . O local de todos os feixes de ordem zero é, então, um cone idêntico com um ápice comum no ponto de intersecção do feixe com a fileira de átomos; E os feixes incidentes e de ordem zero são geradores diametralmente opostos dos dois cones. As direções que satisfazem a equação 4 para as outras ordens difratadas do feixe encontram-se em outros cones com o mesmo ápice comum e os ângulos de semi-ápice apropriados  (Fig. 8). Note-se que
(Fig. 8). Note-se que  =
=  .[8]
.[8]À esquerda do feixe de ordem zero (Fig. 7) estão as ordens negativas do feixe difratado, a ordem -mth fazendo um ângulo  '-
'-  à esquerda com o feixe de ordem zero e um ângulo
à esquerda com o feixe de ordem zero e um ângulo  ' com a fileira de rede, onde:
' com a fileira de rede, onde:
 '-
'-  à esquerda com o feixe de ordem zero e um ângulo
à esquerda com o feixe de ordem zero e um ângulo  ' com a fileira de rede, onde:
' com a fileira de rede, onde: (equação 5)
(equação 5)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Note-se que o ângulo  ' é medido a partir da extremidade positiva da fila de rede. Ângulo
' é medido a partir da extremidade positiva da fila de rede. Ângulo  é sempre menor do que
é sempre menor do que  , quando o ângulo
, quando o ângulo  < 90 °, e os dois ângulos são iguais no caso especial
< 90 °, e os dois ângulos são iguais no caso especial  = 90 º. O local das direções das ordens negativas do feixe difratado é assim uma série de cones à esquerda do cone de ordem zero e tendo o mesmo ápice comum que as ordens positivas. O ângulo interior do cone do semi-ápice
= 90 º. O local das direções das ordens negativas do feixe difratado é assim uma série de cones à esquerda do cone de ordem zero e tendo o mesmo ápice comum que as ordens positivas. O ângulo interior do cone do semi-ápice  ' torna-se o ângulo apical externo quando
' torna-se o ângulo apical externo quando  ' > 90 º. Uma construção trigonométrica e tratamento semelhante ao que leva à equação 4, nos fornece a seguinte equação[8]:
' > 90 º. Uma construção trigonométrica e tratamento semelhante ao que leva à equação 4, nos fornece a seguinte equação[8]:
 ' é medido a partir da extremidade positiva da fila de rede. Ângulo
' é medido a partir da extremidade positiva da fila de rede. Ângulo  é sempre menor do que
é sempre menor do que  , quando o ângulo
, quando o ângulo  < 90 °, e os dois ângulos são iguais no caso especial
< 90 °, e os dois ângulos são iguais no caso especial  = 90 º. O local das direções das ordens negativas do feixe difratado é assim uma série de cones à esquerda do cone de ordem zero e tendo o mesmo ápice comum que as ordens positivas. O ângulo interior do cone do semi-ápice
= 90 º. O local das direções das ordens negativas do feixe difratado é assim uma série de cones à esquerda do cone de ordem zero e tendo o mesmo ápice comum que as ordens positivas. O ângulo interior do cone do semi-ápice  ' torna-se o ângulo apical externo quando
' torna-se o ângulo apical externo quando  ' > 90 º. Uma construção trigonométrica e tratamento semelhante ao que leva à equação 4, nos fornece a seguinte equação[8]:
' > 90 º. Uma construção trigonométrica e tratamento semelhante ao que leva à equação 4, nos fornece a seguinte equação[8]: (equação 6)
(equação 6)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
e
 (equação 7)
(equação 7)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
No caso especial em que o feixe incidente é perpendicular à linha de átomos,  = 90 °, o cone de ordem zero degenera em um disco perpendicular à rede linear e os cones de cada ordem positiva e negativa de difração se tornam simétricos sobre a ordem zero. Para um dado
= 90 °, o cone de ordem zero degenera em um disco perpendicular à rede linear e os cones de cada ordem positiva e negativa de difração se tornam simétricos sobre a ordem zero. Para um dado  e espaçamento interatômico
e espaçamento interatômico  , somente um número limitado de ordens de difração é possível, pois quando
, somente um número limitado de ordens de difração é possível, pois quando  é tal que faz com que o membro direito da equação 4 exceda a unidade (ou - 1 na equação 7) nenhuma solução para
é tal que faz com que o membro direito da equação 4 exceda a unidade (ou - 1 na equação 7) nenhuma solução para  ou
ou  é possível[8].
é possível[8].
 = 90 °, o cone de ordem zero degenera em um disco perpendicular à rede linear e os cones de cada ordem positiva e negativa de difração se tornam simétricos sobre a ordem zero. Para um dado
= 90 °, o cone de ordem zero degenera em um disco perpendicular à rede linear e os cones de cada ordem positiva e negativa de difração se tornam simétricos sobre a ordem zero. Para um dado  e espaçamento interatômico
e espaçamento interatômico  , somente um número limitado de ordens de difração é possível, pois quando
, somente um número limitado de ordens de difração é possível, pois quando  é tal que faz com que o membro direito da equação 4 exceda a unidade (ou - 1 na equação 7) nenhuma solução para
é tal que faz com que o membro direito da equação 4 exceda a unidade (ou - 1 na equação 7) nenhuma solução para  ou
ou  é possível[8].
é possível[8].A equação de Bragg[editar | editar código-fonte]
A Equação 8 é a equação de Bragg para o sistema cúbico. A referência revela que o fator 

x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
na equação 8 é simplesmente o espaçamento interplanar  para o plano (hkl). A equação de Bragg (equação 9) na sua forma geral é então escrita[8]:
para o plano (hkl). A equação de Bragg (equação 9) na sua forma geral é então escrita[8]:
 para o plano (hkl). A equação de Bragg (equação 9) na sua forma geral é então escrita[8]:
para o plano (hkl). A equação de Bragg (equação 9) na sua forma geral é então escrita[8]: (equação 8)
(equação 8)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
e
 (equação 9)
(equação 9)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Uma derivação analítica da equação de Bragg quando realizada para um sistema cristalino de simetria inferior conduz a uma expressão idêntica à equação 8 ou 9, exceto com um termo  mais complicado. Estes são, em todos os casos, o espaçamento inter planar para o plano refletor. Assim, para obter a equação na forma especial para cálculos em um determinado sistema de cristais, é necessário apenas substituir em vez de
mais complicado. Estes são, em todos os casos, o espaçamento inter planar para o plano refletor. Assim, para obter a equação na forma especial para cálculos em um determinado sistema de cristais, é necessário apenas substituir em vez de  a expressão (Tabela 1) para
a expressão (Tabela 1) para  , ou o sistema apropriado[8].
, ou o sistema apropriado[8].
 mais complicado. Estes são, em todos os casos, o espaçamento inter planar para o plano refletor. Assim, para obter a equação na forma especial para cálculos em um determinado sistema de cristais, é necessário apenas substituir em vez de
mais complicado. Estes são, em todos os casos, o espaçamento inter planar para o plano refletor. Assim, para obter a equação na forma especial para cálculos em um determinado sistema de cristais, é necessário apenas substituir em vez de  a expressão (Tabela 1) para
a expressão (Tabela 1) para  , ou o sistema apropriado[8].
, ou o sistema apropriado[8].A explicação de Bragg sobre os efeitos de difração de raios X em termos de "reflexão" de uma pilha de planos atômicos paralelos merece breve consideração, tanto por sua simplicidade quanto por seu interesse histórico. As unidades atômicas ou moleculares em um cristal encontram-se nas interseções de uma estrutura de espaço, que as proeminentes faces de cristal são aquelas mais densamente povoadas com pontos de rede (Átomos ou moléculas), e que, paralelamente a cada face ou plano de cristal possível, há uma série de planos idênticos equidistantes. Quando um feixe de raios X atinge uma face de cristal estendida e é refletido no sentido de Bragg o fenômeno não é uma reflexão de superfície, como com a luz comum. Paralelo à face é uma série efetivamente infinita de planos atômicos equidistantes que os raios X penetram a uma profundidade de vários milhões de camadas antes de ser apreciadamente absorvida. Em cada plano atómico pode considerar-se que uma porção de minuto do feixe é refletida. Para que esses minúsculos feixes refletidos surjam como um único feixe de intensidade apreciável, não devem ser absorvidos ao passar por camadas mais próximas da superfície à medida que emergem, e, muito mais importante, os feixes de camadas sucessivas não devem interferir e destruir uns aos outros. Se as condições podem ser arranjadas para que o reforço, em vez de destruição ocorre, todos os planos da série que não são muito profundas no cristal vai contribuir para a reflexão. Bragg demonstrou estas condições da seguinte maneira. Considere as linhas  etc., da Fig. 9 para representar os traços de uma série de planos atômicos de espaçamento interplanar constante d paralelo a uma face de cristal[8]. AB, A'B 'é um comboio de raios X incidentes de comprimento de onda X incidindo sobre os planos e refletindo na direção CD. Para a onda refletida de B 'para reforçar a refletida em C, ela deve chegar em C em fase com a onda ABC. Este será o caso se a diferença de percurso for um número inteiro de comprimentos de onda, isto é, se
etc., da Fig. 9 para representar os traços de uma série de planos atômicos de espaçamento interplanar constante d paralelo a uma face de cristal[8]. AB, A'B 'é um comboio de raios X incidentes de comprimento de onda X incidindo sobre os planos e refletindo na direção CD. Para a onda refletida de B 'para reforçar a refletida em C, ela deve chegar em C em fase com a onda ABC. Este será o caso se a diferença de percurso for um número inteiro de comprimentos de onda, isto é, se
 etc., da Fig. 9 para representar os traços de uma série de planos atômicos de espaçamento interplanar constante d paralelo a uma face de cristal[8]. AB, A'B 'é um comboio de raios X incidentes de comprimento de onda X incidindo sobre os planos e refletindo na direção CD. Para a onda refletida de B 'para reforçar a refletida em C, ela deve chegar em C em fase com a onda ABC. Este será o caso se a diferença de percurso for um número inteiro de comprimentos de onda, isto é, se
etc., da Fig. 9 para representar os traços de uma série de planos atômicos de espaçamento interplanar constante d paralelo a uma face de cristal[8]. AB, A'B 'é um comboio de raios X incidentes de comprimento de onda X incidindo sobre os planos e refletindo na direção CD. Para a onda refletida de B 'para reforçar a refletida em C, ela deve chegar em C em fase com a onda ABC. Este será o caso se a diferença de percurso for um número inteiro de comprimentos de onda, isto é, se (equação 9)
(equação 9)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Por simples trigonometria
 (equação 10)
(equação 10)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
e  (equação 11)
(equação 11)
 (equação 11)
(equação 11)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
substituição na equação 10,  (equação 12)
(equação 12)
 (equação 12)
(equação 12)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
e  (equação 13).
(equação 13).
 (equação 13).
(equação 13).Esta é a equação de Bragg, também conhecida como a lei de Bragg (equação 13). Para um cristal de um determinado espaçamento  , e para um dado comprimento de onda
, e para um dado comprimento de onda  , as várias ordens
, as várias ordens  de reflexão ocorrem apenas nos valores precisos do ângulo
de reflexão ocorrem apenas nos valores precisos do ângulo  que satisfazem a equação 13. Em outros ângulos não há feixe refletido devido a interferência. Isto está em marcado contraste com a reflexão de um feixe de luz a partir de uma superfície de metal polido, que pode ter lugar ao longo de uma grande faixa angular contínua. O ponto de vista da reflexão proporciona assim uma Imagem de difração em cristais, e tem sido amplamente utilizado[8].
que satisfazem a equação 13. Em outros ângulos não há feixe refletido devido a interferência. Isto está em marcado contraste com a reflexão de um feixe de luz a partir de uma superfície de metal polido, que pode ter lugar ao longo de uma grande faixa angular contínua. O ponto de vista da reflexão proporciona assim uma Imagem de difração em cristais, e tem sido amplamente utilizado[8].
 , e para um dado comprimento de onda
, e para um dado comprimento de onda  , as várias ordens
, as várias ordens  de reflexão ocorrem apenas nos valores precisos do ângulo
de reflexão ocorrem apenas nos valores precisos do ângulo  que satisfazem a equação 13. Em outros ângulos não há feixe refletido devido a interferência. Isto está em marcado contraste com a reflexão de um feixe de luz a partir de uma superfície de metal polido, que pode ter lugar ao longo de uma grande faixa angular contínua. O ponto de vista da reflexão proporciona assim uma Imagem de difração em cristais, e tem sido amplamente utilizado[8].
que satisfazem a equação 13. Em outros ângulos não há feixe refletido devido a interferência. Isto está em marcado contraste com a reflexão de um feixe de luz a partir de uma superfície de metal polido, que pode ter lugar ao longo de uma grande faixa angular contínua. O ponto de vista da reflexão proporciona assim uma Imagem de difração em cristais, e tem sido amplamente utilizado[8].Os instrumentos tradicionais de medida são o difratômetro (método de pó) e as câmaras de monocristais, estas últimas atualmente com seu uso restrito a situações específicas para determinação de parâmetros cristalográficos. No difratômetro tradicional a captação do eixo difratado é feita por meio de um detector, segundo um arranjo geométrico conhecido como Bragg-Brentano, que habilita a obtenção do ângulo  .[8]
.[8]
 .[8]
.[8]O feixe difratado é normalmente expresso através de picos que se destacam do background (ou linha de base), registrados num espectro de intensidade versus o ângulo  , constituindo o padrão difratométrico ou difratograma. O padrão difratométrico representa uma coleção de perfis de reflexões ( difrações ) individuais ( ou picos difratados), cada qual com sua altura, largura, área integrada, posição angular e caudas que decaem gradualmente a medida que se distanciam da posição de altura máxima do pico. A intensidade integrada é proporcional à intensidade de Bragg, I(hkI). A identificação das substâncias cristalinas ( através do método de pó) é obtida através da comparação do difratograma com padrões difratométricos de fases individuais disponibilizadas pelo ICDD ( International Center for Diffraction Data, antigo JCPDS-Joint Committe of Powder Diffraction Standards)[8].
, constituindo o padrão difratométrico ou difratograma. O padrão difratométrico representa uma coleção de perfis de reflexões ( difrações ) individuais ( ou picos difratados), cada qual com sua altura, largura, área integrada, posição angular e caudas que decaem gradualmente a medida que se distanciam da posição de altura máxima do pico. A intensidade integrada é proporcional à intensidade de Bragg, I(hkI). A identificação das substâncias cristalinas ( através do método de pó) é obtida através da comparação do difratograma com padrões difratométricos de fases individuais disponibilizadas pelo ICDD ( International Center for Diffraction Data, antigo JCPDS-Joint Committe of Powder Diffraction Standards)[8].
 , constituindo o padrão difratométrico ou difratograma. O padrão difratométrico representa uma coleção de perfis de reflexões ( difrações ) individuais ( ou picos difratados), cada qual com sua altura, largura, área integrada, posição angular e caudas que decaem gradualmente a medida que se distanciam da posição de altura máxima do pico. A intensidade integrada é proporcional à intensidade de Bragg, I(hkI). A identificação das substâncias cristalinas ( através do método de pó) é obtida através da comparação do difratograma com padrões difratométricos de fases individuais disponibilizadas pelo ICDD ( International Center for Diffraction Data, antigo JCPDS-Joint Committe of Powder Diffraction Standards)[8].
, constituindo o padrão difratométrico ou difratograma. O padrão difratométrico representa uma coleção de perfis de reflexões ( difrações ) individuais ( ou picos difratados), cada qual com sua altura, largura, área integrada, posição angular e caudas que decaem gradualmente a medida que se distanciam da posição de altura máxima do pico. A intensidade integrada é proporcional à intensidade de Bragg, I(hkI). A identificação das substâncias cristalinas ( através do método de pó) é obtida através da comparação do difratograma com padrões difratométricos de fases individuais disponibilizadas pelo ICDD ( International Center for Diffraction Data, antigo JCPDS-Joint Committe of Powder Diffraction Standards)[8].Relação entre a estrutura cristalina e os dados de raios X: posições de pico, intensidades e larguras[editar | editar código-fonte]
Posições de pico[editar | editar código-fonte]
Usando a Lei de Bragg, as posições de pico podem ser teoricamente calculadas.[9]
 (equação 14)
(equação 14)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Para uma célula unitária cúbica:
 onde
onde  e
e  é o parâmetro de célula.
é o parâmetro de célula.x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Assim, o valor medido  pode estar relacionado com os parâmetros da célula.
pode estar relacionado com os parâmetros da célula.
 pode estar relacionado com os parâmetros da célula.
pode estar relacionado com os parâmetros da célula.Intensidade do pico[editar | editar código-fonte]
O fator de estrutura, de uma reflexão,
de uma reflexão,  , é dependente do tipo de átomos e suas posições
, é dependente do tipo de átomos e suas posições  na célula unitária.[9]
na célula unitária.[9]
 de uma reflexão,
de uma reflexão,  , é dependente do tipo de átomos e suas posições
, é dependente do tipo de átomos e suas posições  na célula unitária.[9]
na célula unitária.[9] (equação 15)
(equação 15)x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
 é o fator de dispersão para o átomo
é o fator de dispersão para o átomo  e está relacionado ao seu número atômico.
e está relacionado ao seu número atômico.A intensidade de um pico  é dada por:
é dada por:
 é dada por:
é dada por:
x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
As diferenças de intensidade se relacionam com mudanças na química (fator de dispersão). No entanto, mais comumente para amostras multifásicas, as alterações nas intensidades estão relacionadas com a quantidade de cada fase presente na amostra. São necessários fatores de calibração adequados para realizar a análise de fase quantitativa.
Largura do pico[editar | editar código-fonte]
A largura de pico β em radianos é inversamente proporcional ao tamanho do cristalito  perpendicular ao plano
perpendicular ao plano 
 perpendicular ao plano
perpendicular ao plano 
 (equação 16 - Equação de Scherrer)[9]
(equação 16 - Equação de Scherrer)[9]x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC]. + FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA. + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE ,
,  + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL +
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCKX
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Fatores que afetam as intensidades de difração[editar | editar código-fonte]
Os dados que geram os difratogramas são afetados não só por sobreposição dos planos de reflexão como também por efeitos físicos, instrumentais e por características de cada amostra[8]. Entre os fatores estão:
- O fator de polarização;
- Fatores de Lorentz e velocidade;
- O fator temperatura;
- O fator de dispersão atômica;
- O fator de estrutura;
- O fator de multiplicidade;
- O fator de absorção;
O fator de polarização é de natureza física, causado pela ausência de parelelismo entre o feixe incidente e os planos de reflexão. Esse fator provoca na onda difratada um decréscimo na intensidade em função do ângulo de incidência. Fatores relacionados à preparação das amostras são considerados as maiores fontes de erros para as três informações fundamentais de cada reflexão: posição angular, intensidade e perfil de pico. O deslocamento da amostra devido à fuga do ponto focal óptica do difratômetro pode ocorrer devido a dificuldade de prensagem do pó na altura dos suportes compatíveis com o arranjo geométrico do equipamento (geometria de bragg), provocando um deslocamento na posição dos picos e um alargamento assimétrico dos perfis. Tais fatores reforçam a importância da configuração do equipamento e de sua calibração, minimizando seu efeito nas intensidades de picos de difratograma[8].
O feixe é um conjunto de objetos paralelos colocados perto um do outro, como numa vassoura de gravetos onde eles são amarrados por uma corda, vindo daí a palavra "faxina".[1]
Na Física, este termo, é encontrado na Óptica, o estudo da luz, na Física de partículas, cujo feixe de luz, constituido de um conjunto de raios de luz paralelos, convergentes e ou divergentes[2], e em aceleradores de partículas, partículas, íons de ambas cargas elétricas ( partículas com carga elétrica )[3] e moléculas são aceleradas, referir-se a este feixe compacto que se fala de um pacote de partículas que circulam num acelerador.[4]
Um feixe é caracterizado então pela matéria corpuscular atômica que o forma, pelo nível de sua energia cinética  (ou velocidade
(ou velocidade  ) e o número de partículas por unidade de tempo
) e o número de partículas por unidade de tempo  .[5] Se a carga da matéria corpuscular atômica for
.[5] Se a carga da matéria corpuscular atômica for  , logo há uma relação direta com a corrente elétrica total do feixe,
, logo há uma relação direta com a corrente elétrica total do feixe,  , e o fluxo
, e o fluxo  :
:
 (ou velocidade
(ou velocidade  ) e o número de partículas por unidade de tempo
) e o número de partículas por unidade de tempo  .[5] Se a carga da matéria corpuscular atômica for
.[5] Se a carga da matéria corpuscular atômica for  , logo há uma relação direta com a corrente elétrica total do feixe,
, logo há uma relação direta com a corrente elétrica total do feixe,  , e o fluxo
, e o fluxo  :
:RELATIVIDADE GRACELI DE Efeito do observador (física) NO SDCTIE GRACELI.
segunda-feira, 18 de novembro de 2019
Na física, o efeito do observador são as mudanças que o ato de observação irá fazer em um fenômeno que está sendo observado. Este é muitas vezes o resultado de instrumentos que, por necessidade, alteram o estado do que medem de alguma maneira. Esse efeito pode ser observado em muitos domínios da física e muitas vezes pode ser reduzido a resultados insignificantes usando diferentes instrumentos ou técnicas de observação.Na mecânica quântica, há um equívoco comum de que é somente a mente de um observador consciente que causa o efeito observador em processos quânticos. Esse erro está enraizado em um mal-entendido da função de onda quântica ψ[1][2][3] e do processo de medição quântica.[4][5][6][7]Física de partículas[editar | editar código-fonte]
Para que um elétron se torne detectável, um fóton deve primeiro interagir com ele, e essa interação inevitavelmente mudará o caminho desse elétron. Também é possível que outros meios de medição, menos diretos, afetem o elétron. É necessário distinguir claramente entre o valor medido de uma quantidade e o valor resultante do processo de medição. Em particular, uma medida do momento não é repetível em curtos intervalos de tempo. Uma fórmula (unidimensional, para simplificar) relativa às quantidades envolvidas, por conta de Niels Bohr é dada por- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Onde- Δpx é incerteza no valor medido do momento,
- Δt é a duração da medição,
- vx é a velocidade da partícula antes medição.,
- v '
x é a velocidade da partícula depois medição, - ħ é a constante de Planck reduzida.
A quantidade de movimento medida do elétron é então relacionada a vx, enquanto seu momento após a medição está relacionado a v′x. Este é o melhor cenário.[8]O efeito Hall quântico, também chamado de efeito Hall quântico inteiro, é uma versão do efeito Hall em mecânica quântica, observado em sistemas bidimensionais de elétrons[nota 1] [1][2] submetidos a baixas temperaturas e fortes campos magnéticos, em que a condutividade Hallsofre certas transições quânticas para assumir valores quantizados:
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
A dualidade partícula-onda foi enunciada pela primeira vez em 1924, pelo físico francês Louis-Victor de Broglie, que anunciou que os elétrons apresentavam características tanto ondulatórias como corpusculares, comportando-se de um ou outro modo dependendo do experimento específico. A experiência de Young (experiência da dupla fenda) exemplifica de maneira sensível o comportamento ondulatório do elétron; e pelo que já se conhecia do mesmo como partícula - a citarem-se os experimentos realizados com o tubo de Crookes, e outros - concluiu-se a dualidade onda-partícula deste ente, visto que a difração em fenda dupla é uma propriedade notoriamente ondulatória.[1]De Broglie fundou seu raciocínio inicialmente na intuição e nos conhecimentos acerca do efeito fotoelétrico para chegar a esta conclusão. Durante os estudos de Albert Einstein acerca do efeito fotoelétrico - estudos que lhe renderam o prêmio Nobel - ele havia concluído que os fótons que atuavam no efeito fotoelétrico exibiam todas as propriedades esperadas de um feixe de partículas, comportando-se cada qual como uma partícula com energia E=h•f, onde f representa a frequência da onda eletromagnética associada aos fótons em consideração. Einstein concluiu desta forma que, em determinados processos, as ondas se comportam como se fossem corpúsculos. De Broglie imaginou então o inverso, ou seja, se ondas se comportam como partículas, porque não esperar que partículas se comportem como ondas? Levando sua ideia a cabo e confrontando-a com dados empíricos o físico francês foi capaz de relacionar com sucesso o comprimento de onda associado ao comportamento ondulatório da "partícula" com sua massa mediante a fórmula λ=h/p, onde p representa o módulo do vetor quantidade de movimento, ou seja, o produto da massa pelo módulo da velocidade (m•v) do ente; h representa a Constante de Planck, e λ é o comprimento de onda associado.[1]xFUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Observando-se a fórmula verifica-se facilmente que, à medida que a massa ou sua velocidade aumenta, diminui-se consideravelmente o comprimento de onda. Os corpos macroscópicos têm associada uma onda, porém sua massa é tão grande que pode-se afirmar que apresentam um comprimento de onda desprezível, porém não nulo. Embora no mundo macroscópico tais efeitos ondulatórios sejam por tal imperceptíveis, no mundo subatômico estes certamente não o são, e por tal, na hora de se falar sobre "partículas" atômicas é muito importante se consPode-se exprimir o princípio da incerteza nos seguintes termos:O produto da incerteza associada ao valor de uma coordenada xi e a incerteza associada ao seu correspondente momento linear pi não pode ser inferior, em grandeza, à constante reduzida de Planck.[4] Em termos matemáticos, exprime-se assim:x FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
A explicação disso não é fácil de se entender, e fala mesmo em favor da intuição, embora o raciocínio clássico e os aspectos formais da análise matemática tenham levado os cientistas a pensarem diferentemente por muito tempo. Quando se quer encontrar a posição de um elétron, por exemplo, é necessário fazê-lo interagir com algum instrumento de medida, direta ou indiretamente. Por exemplo, faz-se incidir sobre ele algum tipo de radiação. Tanto faz aqui que se considere a radiação do modo clássico - constituída por ondas eletromagnéticas - ou do modo quântico - constituída por fótons. Caso se queira determinar a posição do elétron, é necessário que a radiação tenha comprimento de onda da ordem da incerteza com que se quer determinar a posição.[5]Neste caso, quanto menor for o comprimento de onda (maior frequência), maior será a precisão. Contudo, maior será a energia cedida pela radiação (onda ou fóton) em virtude da relação de Planck entre energia e frequência da radiaçãox FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
e o elétron sofrerá um recuo tanto maior quanto maior for essa energia, em virtude do efeito Compton. Como consequência, a velocidade sofrerá uma alteração não de todo previsível, ao contrário do que afirmaria a mecânica clássica.Argumentos análogos poderiam ser usados para se demonstrar que ao se medir a velocidade com precisão, alterar-se-ia a posição de modo não totalmente previsível.Resumidamente, pode-se dizer que tudo se passa de forma que quanto mais precisamente se medir uma grandeza, forçosamente mais será imprecisa a medida da grandeza correspondente, chamada de canonicamente conjugada.Algumas pessoas consideram mais fácil o entendimento através da analogia. Para se descobrir a posição de uma bola de plástico dentro de um quarto escuro, podemos emitir algum tipo de radiação e deduzir a posição da bola através das ondas que "batem" na bola e voltam. Se quisermos calcular a velocidade de um automóvel, podemos fazer com que ele atravesse dois feixes de luz, e calcular o tempo que ele levou entre um feixe e outro. Nem radiação nem a luz conseguem interferir de modo significativo na posição da bola, nem alterar a velocidade do automóvel. Mas podem interferir muito tanto na posição quanto na velocidade de um elétron, pois aí a diferença de tamanho entre o fóton de luz e o elétron é pequena. Seria, mais ou menos, como fazer o automóvel ter de atravessar dois troncos de árvores (o que certamente alteraria sua velocidade), ou jogar água dentro do quarto escuro, para deduzir a localização da bola através das pequenas ondas que baterão no objeto e voltarão; mas a água pode empurrar a bola mais para a frente, alterando sua posição. Desta forma torna-se impossível determinar a localização real desta bola, pois a própria determinação mudará a sua posição. Apesar disto, a sua nova posição pode ser ainda deduzida, calculando o quanto a bola seria empurrada sabendo a força das ondas obtendo-se uma posição provável da bola e sendo provável que a bola esteja localizada dentro daquela área.Assinar: Postagens (Atom)RELATIVIDADE SDCTIE GRACELI SOBRE Espalhamento
quinta-feira, 28 de novembro de 2019
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI. =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Denomina-se espalhamento o processo físico em que determinada forma de energia (radiação eletromagnética, partículas em movimento ou som) ao se propagar em uma trajetória linear sofre uma alteração de caminho devido às interações com o meio pelo qual atravessam. O espalhamento também inclui o desvio da radiação por reflexão. Reflexões que sofrem espalhamento são freqüentemente chamadas de reflexões difusas e reflexões especulares (semelhantes a espelhos).No caso de espalhamento de partículas, é resultado de colisões entre moléculas, átomos, elétrons, fótons e outras partículas. Exemplos incluem: dispersão de raios cósmicos na atmosfera superior da Terra; colisões de partículas dentro de aceleradores de partículas; espalhamento de elétrons por átomos de gás em lâmpadas fluorescentes; e espalhamento de nêutrons dentro de reatores nucleares.No meio de propagação, os tipos de não uniformidade que podem causar espalhamento, às vezes conhecidos como dispersores ou centros de dispersão, são numerosos demais para serem listados, mas uma pequena amostra inclui partículas, bolhas, gotículas, flutuações de densidade em fluidos, cristalitos em sólidos policristalinos, defeitos em sólidos monocristalinos rugosidade superficial, células em organismos e fibras têxteis em roupas. Os efeitos de tais características no caminho de quase qualquer tipo de onda de propagação ou partícula móvel podem ser descritos na estrutura da teoria de espalhamento.Algumas áreas onde o espalhamento e a teoria de espalhamento são significativas incluem sensoriamento por radar, ultrassom médico, inspeção de wafer semicondutor, monitoramento de processo de polimerização, revestimento acústico, comunicações de espaço livre e imagens geradas por computador. A teoria da dispersão de partícula-partícula é importante em áreas como física de partículas, física atômica, molecular e óptica, física nuclear e astrofísica.Espalhamento simples e múltiplo[editar | editar código-fonte]
Quando a radiação é apenas espalhada por um centro de dispersão localizado, isso é chamado de espalhamento único. É muito comum que os centros de dispersão sejam agrupados; nesses casos, a radiação pode se espalhar muitas vezes, no que é conhecido como espalhamento múltipla. A principal diferença entre os efeitos do espalhamento simples e múltiplo é que o primeiro pode ser tratado como um fenômeno aleatório e o segundo pode ser modelado como um processo mais determinístico onde os resultados combinados de um grande número de eventos de dispersão tendem a uma média. O espalhamento múltiplo pode, portanto, ser bem modelado com a teoria de espalhamento.Como a localização de um único centro de dispersão geralmente não é bem conhecida em relação ao caminho da radiação, o resultado, que tende a depender fortemente da trajetória exata de entrada, parece aleatório para um observador. Este tipo de espalhamento seria exemplificado por um elétron sendo disparado em um núcleo atômico. Neste caso, a posição exata do átomo em relação ao caminho do elétron é desconhecida e seria imensurável, então a trajetória exata do elétron após a colisão não pode ser prevista. O espalhamento único é, portanto, freqüentemente descrito por distribuições de probabilidade. A luz zodiacal é um brilho fraco e difuso, visível no céu noturno. O fenômeno deriva da dispersão da luz solar pela poeira interplanetária espalhada pelo plano do Sistema Solar.[3]Com o espalhamento múltiplo, a aleatoriedade da interação tende a ser calculada através do grande número de eventos de espalhamento, de modo que o caminho final da radiação parece ser uma distribuição determinística da intensidade. Isto é exemplificado por um feixe de luz que passa através da névoa espessa. O espalhamento múltiplo é altamente análogo à difusão, e os termos dispersão e difusão múltipla são intercambiáveis em muitos contextos. Elementos ópticos projetados para produzir dispersão múltipla são, portanto, conhecidos como difusores.Nem todo espalhamento único é aleatório. Um feixe de laser bem controlado pode ser posicionado exatamente para dispersar uma partícula microscópica com um resultado determinístico, por exemplo. Tais situações também são encontradas na dispersão de radar, onde os alvos tendem a ser objetos macroscópicos, como pessoas ou aeronaves.Da mesma forma, o espalhamento múltiplo às vezes pode ter resultados aleatórios, particularmente com radiação coerente. As flutuações aleatórias na intensidade dispersa da radiação coerente são chamadas de speckles. O speckle também ocorre se várias partes de uma onda coerente se espalham de diferentes centros. Em certas circunstâncias raras, o espalhamento múltiplo pode envolver apenas um pequeno número de interações, de modo que a aleatoriedade não seja completamente calculada. Estes sistemas são considerados alguns dos mais difíceis de modelar com precisão.A descrição do espalhamento e a distinção entre espalhamento único e múltiplo estão intimamente relacionados à dualidade onda-partícula.
A luz zodiacal é um brilho fraco e difuso, visível no céu noturno. O fenômeno deriva da dispersão da luz solar pela poeira interplanetária espalhada pelo plano do Sistema Solar.[3]Com o espalhamento múltiplo, a aleatoriedade da interação tende a ser calculada através do grande número de eventos de espalhamento, de modo que o caminho final da radiação parece ser uma distribuição determinística da intensidade. Isto é exemplificado por um feixe de luz que passa através da névoa espessa. O espalhamento múltiplo é altamente análogo à difusão, e os termos dispersão e difusão múltipla são intercambiáveis em muitos contextos. Elementos ópticos projetados para produzir dispersão múltipla são, portanto, conhecidos como difusores.Nem todo espalhamento único é aleatório. Um feixe de laser bem controlado pode ser posicionado exatamente para dispersar uma partícula microscópica com um resultado determinístico, por exemplo. Tais situações também são encontradas na dispersão de radar, onde os alvos tendem a ser objetos macroscópicos, como pessoas ou aeronaves.Da mesma forma, o espalhamento múltiplo às vezes pode ter resultados aleatórios, particularmente com radiação coerente. As flutuações aleatórias na intensidade dispersa da radiação coerente são chamadas de speckles. O speckle também ocorre se várias partes de uma onda coerente se espalham de diferentes centros. Em certas circunstâncias raras, o espalhamento múltiplo pode envolver apenas um pequeno número de interações, de modo que a aleatoriedade não seja completamente calculada. Estes sistemas são considerados alguns dos mais difíceis de modelar com precisão.A descrição do espalhamento e a distinção entre espalhamento único e múltiplo estão intimamente relacionados à dualidade onda-partícula.Teoria de espalhamento[editar | editar código-fonte]
Artigo principal: Teoria de espalhamentoA teoria da dispersão ou espalhamento é uma estrutura para estudar e compreender a dispersão de ondas e partículas. Prosaicamente, o espalhamento de onda corresponde à colisão e dispersão de uma onda com algum objeto material, por exemplo, a luz solar espalhada pelas gotas de chuva para formar um arco-íris. A dispersão também inclui a interação de bolas de bilhar em uma mesa, o espalhamento de Rutherford (ou mudança de ângulo) de partículas alfa por núcleos de ouro, o espalhamento de Bragg (ou difração de elétrons) e raios X por um aglomerado de átomos e o espalhamento inelástico de um fragmento de fissão ao atravessar uma folha fina. Mais precisamente, o espalhamento consiste no estudo de como soluções de equações diferenciais parciais, propagando-se livremente "no passado distante", se juntam e interagem umas com as outras ou com uma condição de contorno, e então se propagam "para o futuro distante".Coeficiente de espalhamento[editar | editar código-fonte]
O coeficiente de espalhamento μs [cm-1] descreve um meio que contém muitas partículas espalhadoras em uma concentração descrita por uma densidade volumétrica ρ [cm3]; o coeficiente de espalhamento é essencialmente a seção de choque σs por unidade de volume do meio.[4][5]x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.O recíproco do coeficiente de espalhamento pode ser entendido como a distancia média que a partícula viaja antes de interagir com o meio, ou seja, ser espalhado.As ondas eletromagnéticas são uma das formas de radiação mais conhecidas e mais comumente encontradas que sofrem dispersão. A dispersão das ondas de luz e rádio (especialmente no radar ) é particularmente importante. Vários aspectos diferentes da dispersão eletromagnética são suficientemente distintos para ter nomes convencionais. As principais formas de dispersão elástica da luz (envolvendo transferência de energia desprezível) são a dispersão de Rayleigh e Mie . A dispersão inelástica inclui a dispersão de Brillouin , a dispersão de Raman , a dispersão inelástica de raios X e a dispersão de Compton .A dispersão da luz é um dos dois principais processos físicos que contribuem para a aparência visível da maioria dos objetos, sendo o outro a absorção. As superfícies descritas como brancas devem sua aparência a múltiplas dispersões de luz por não homogeneidades internas ou de superfície no objeto, por exemplo, pelos limites de cristais microscópicos transparentes que compõem uma pedra ou pelas fibras microscópicas em uma folha de papel. De um modo mais geral, o brilho (ou brilho ou brilho ) da superfície é determinado por espalhamento. As superfícies com alta dispersão são descritas como opacas ou com acabamento fosco, enquanto a ausência de dispersão da superfície leva a uma aparência brilhante, como no metal ou pedra polida.A absorção espectral, a absorção seletiva de certas cores, determina a cor da maioria dos objetos com alguma modificação por espalhamento elástico . A cor azul aparente das veias na pele é um exemplo comum em que a absorção espectral e a dispersão desempenham papéis importantes e complexos na coloração. A dispersão da luz também pode criar cores sem absorção, geralmente tons de azul, como no céu ( dispersão de Rayleigh ), na íris azul humana e nas penas de alguns pássaros (Prum et al. 1998). No entanto, a dispersão de luz ressonante nas nanopartículas pode produzir muitos tons diferentes altamente saturados e vibrantes, especialmente quando a ressonância plasmônica de superfície está envolvida (Roqué et al. 2006).Os modelos de espalhamento de luz podem ser divididos em três domínios com base em um parâmetro de tamanho sem dimensão, α que é definido como:- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde π D p é a circunferência de uma partícula e λ é o comprimento de onda da radiação incidente. Com base no valor de α , esses domínios são:- α 1: espalhamento de Rayleigh (partícula pequena comparada ao comprimento de onda da luz);
- α 1: dispersão Mie (partícula do mesmo tamanho que o comprimento de onda da luz, válida apenas para esferas);
- α ≫ 1: espalhamento geométrico (partícula muito maior que o comprimento de onda da luz).
A dispersão de Rayleigh é um processo no qual a radiação eletromagnética (incluindo a luz) é dispersa por um pequeno volume esférico de índices de refração variantes, como partículas, bolhas, gotículas ou mesmo uma flutuação de densidade. Este efeito foi modelado pela primeira vez com sucesso por Lord Rayleigh , de quem recebe o nome. Para que o modelo de Rayleigh seja aplicado, a esfera deve ter um diâmetro muito menor que o comprimento de onda ( λ) da onda dispersa; normalmente, o limite superior é considerado em cerca de 1/10 do comprimento de onda. Nesse regime de tamanho, a forma exata do centro de dispersão geralmente não é muito significativa e pode frequentemente ser tratada como uma esfera de volume equivalente. A dispersão inerente à qual a radiação passa através de um gás puro é devida a flutuações microscópicas da densidade à medida que as moléculas de gás se movem, que são normalmente pequenas o suficiente em escala para a aplicação do modelo de Rayleigh. Esse mecanismo de dispersão é a principal causa da cor azul do céu da Terra em um dia claro, pois os comprimentos de onda azuis mais curtos da luz solar que passam no céu são mais dispersos do que os comprimentos de ondas vermelhos mais longos, de acordo com o famoso 1 / λ 4 de Rayleighrelação. Juntamente com a absorção, essa dispersão é uma das principais causas da atenuação da radiação pela atmosfera . O grau de espalhamento varia em função da razão entre o diâmetro das partículas e o comprimento de onda da radiação, juntamente com muitos outros fatores, incluindo polarização , ângulo e coerência .Para diâmetros maiores, o problema da dispersão eletromagnética por esferas foi resolvido pela primeira vez por Gustav Mie , e a dispersão por esferas maiores que a faixa de Rayleigh é, portanto, geralmente conhecida como dispersão de Mie . No regime de Mie, a forma do centro de dispersão se torna muito mais significativa e a teoria se aplica apenas a esferas e, com algumas modificações, esferóides e elipsóides . Existem soluções de forma fechada para dispersão por outras formas simples, mas nenhuma solução geral de forma fechada é conhecida para formas arbitrárias.A dispersão de Mie e Rayleigh é considerada um processo de dispersão elástica, no qual a energia (e, portanto, o comprimento de onda e a frequência) da luz não é substancialmente alterada. No entanto, a radiação eletromagnética dispersa pelos centros de dispersão em movimento passa por um deslocamento Doppler , que pode ser detectado e usado para medir a velocidade do (s) centro (s) de dispersão em formas de técnicas como lidar e radar . Essa mudança envolve uma ligeira mudança na energia.Em valores da razão entre o diâmetro das partículas e o comprimento de onda superior a 10, as leis da óptica geométrica são suficientes para descrever a interação da luz com a partícula e, nesse ponto, a interação geralmente não é descrita como dispersão.Para modelagem de espalhamento nos casos em que os modelos de Rayleigh e Mie não se aplicam, como partículas de formato irregular, existem muitos métodos numéricos que podem ser usados. Os mais comuns são os métodos de elementos finitos que resolvem as equações de Maxwell para encontrar a distribuição do campo eletromagnético disperso. Existem pacotes de software sofisticados que permitem ao usuário especificar o índice ou índices de refração do recurso de dispersão no espaço, criando um modelo bidimensional ou às vezes tridimensional da estrutura. Para estruturas relativamente grandes e complexas, esses modelos geralmente requerem tempos de execução substanciais em um computador.Condição de Bragg [ editar ]
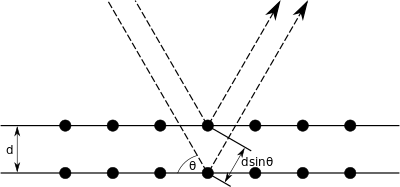 Difração de Bragg. Dois feixes com comprimento de onda e fase idênticos se aproximam de um sólido cristalino e são dispersos em dois átomos diferentes dentro dele. A viga inferior percorre um comprimento extra de 2 d sen θ . A interferência construtiva ocorre quando esse comprimento é igual a um múltiplo inteiro do comprimento de onda da radiação.A difração de Bragg ocorre quando a radiação, com um comprimento de onda comparável aos espaçamentos atômicos, é dispersada de maneira especular pelos átomos de um sistema cristalino e sofre interferência construtiva. Para um sólido cristalino, as ondas são dispersas a partir de planos de treliça separados pela distância interplanar d . Quando as ondas dispersas interferem construtivamente, elas permanecem em fase, pois a diferença entre os comprimentos do caminho das duas ondas é igual a um múltiplo inteiro do comprimento de onda. A diferença de caminho entre duas ondas que sofrem interferência é dada por 2 d sen θ , onde θ é o ângulo de visão (veja a figura à direita e observe que isso difere da convenção na lei de Snell, em que θ é medido a partir da superfície normal). O efeito da interferência construtiva ou destrutiva se intensifica devido ao efeito cumulativo da reflexão em sucessivos planos cristalográficos da rede cristalina (como descrito pela notação de Miller ). Isso leva à lei de Bragg, que descreve a condição em θ para que a interferência construtiva seja mais forte: [5]
Difração de Bragg. Dois feixes com comprimento de onda e fase idênticos se aproximam de um sólido cristalino e são dispersos em dois átomos diferentes dentro dele. A viga inferior percorre um comprimento extra de 2 d sen θ . A interferência construtiva ocorre quando esse comprimento é igual a um múltiplo inteiro do comprimento de onda da radiação.A difração de Bragg ocorre quando a radiação, com um comprimento de onda comparável aos espaçamentos atômicos, é dispersada de maneira especular pelos átomos de um sistema cristalino e sofre interferência construtiva. Para um sólido cristalino, as ondas são dispersas a partir de planos de treliça separados pela distância interplanar d . Quando as ondas dispersas interferem construtivamente, elas permanecem em fase, pois a diferença entre os comprimentos do caminho das duas ondas é igual a um múltiplo inteiro do comprimento de onda. A diferença de caminho entre duas ondas que sofrem interferência é dada por 2 d sen θ , onde θ é o ângulo de visão (veja a figura à direita e observe que isso difere da convenção na lei de Snell, em que θ é medido a partir da superfície normal). O efeito da interferência construtiva ou destrutiva se intensifica devido ao efeito cumulativo da reflexão em sucessivos planos cristalográficos da rede cristalina (como descrito pela notação de Miller ). Isso leva à lei de Bragg, que descreve a condição em θ para que a interferência construtiva seja mais forte: [5]- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde n é um número inteiro positivo e λ é o comprimento de onda da onda incidente. Observe que as partículas em movimento, incluindo elétrons , prótons e nêutrons , têm um comprimento de onda associado chamado comprimento de onda de De Broglie . Um padrão de difração é obtido medindo a intensidade das ondas dispersas em função do ângulo de dispersão. Intensidades muito fortes conhecidas como picos de Bragg são obtidas no padrão de difração nos pontos em que os ângulos de dispersão satisfazem a condição de Bragg. Como mencionado na introdução, essa condição é um caso especial das equações de Laue mais gerais, e as equações de Laue podem ser mostradas para reduzir à condição de Bragg sob suposições adicionais.O fenômeno da difração de Bragg por uma treliça de cristal compartilha características semelhantes às da interferência de película fina , que tem uma condição idêntica no limite em que os índices de refração do meio circundante (por exemplo, ar) e do meio interferente (por exemplo, óleo) são iguais.Por uma questão de simplicidade, apenas a forma original do CM - formulada para corpos perfeitamente condutores eletricamente (PEC) em espaço livre - será tratada neste artigo. As quantidades eletromagnéticas serão representadas apenas como imagens de Fourier no domínio da frequência . O medidor de Lorenz é usado.A dispersão de uma onda eletromagnética em um corpo PEC é representada através de uma condição de contorno no corpo PEC, a saber- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
comrepresentando normal unitário da superfície do PEC,
representando a intensidade do campo elétrico incidente, e
representando a intensidade do campo elétrico espalhado definido como
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
esendo número de onda . O operador integro-diferencial
é aquele a ser diagonalizado através dos modos característicos.
A equação governante da decomposição CM é- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
come
sendo partes reais e imaginárias do operador de impedância
, respectivamente, definidos como
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
O resultado de (1) é um conjunto de modos característicos,
, acompanhado por números de características associados
. Claramente, (1) é um problema generalizado de autovalor , que, no entanto, não pode ser resolvido analiticamente (exceto por alguns corpos canônicos [11] ). Portanto, a solução numérica descrita no parágrafo a seguir é comumente empregada.
Matrix formulação [ editar ]
Discretizaçãodo corpo do espalhador
para dentro
subdomínios como
e usando um conjunto de funções contínuas linearmente independentes por peça
,
, permite densidade de corrente
para ser representado como
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
O problema do autovalor (1) é então reformulado em sua forma matricial- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
que pode ser facilmente resolvido usando, por exemplo, a decomposição generalizada de Schur ou o método Arnoldi implicitamente reiniciado, produzindo um conjunto finito de coeficientes de expansãoe números de características associados
. As propriedades da decomposição CM são investigadas abaixo.
Propriedades [ editar ]
As propriedades da decomposição do CM são demonstradas em sua forma matricial.Primeiro, lembre-se de que as formas bilinearese- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde sobrescritodenota a transposição hermitiana e onde
representa uma distribuição arbitrária de corrente de superfície, corresponde à potência irradiada e à potência líquida reativa, [12] respectivamente. As seguintes propriedades podem ser facilmente destiladas:
- A matriz de ponderação
é teoricamente positivo definido e
é indefinido. O quociente de Rayleigh
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
abrange o intervalo dee indica se o modo característico é capacitivo (
), indutivo (
) ou em ressonância (
) Na realidade, o quociente de Rayleigh é limitado pela dinâmica numérica da precisão da máquina usada e o número de modos encontrados corretamente é limitado.
- Os números das características evoluem com frequência, ou seja,
, eles podem se cruzar ou podem ser os mesmos (no caso de degenerescências [13] ). Por esse motivo, o rastreamento de modos é frequentemente aplicado para obter curvas suaves
. [14] [15] [16] [17] [18] Infelizmente, esse processo é parcialmente heurístico e os algoritmos de rastreamento ainda estão longe da perfeição. [11]
- Os modos característicos podem ser escolhidos como funções com valor real,
. Em outras palavras, os modos característicos formam um conjunto de correntes equipases.
- A decomposição do CM é invariável em relação à amplitude dos modos característicos. Este fato é usado para normalizar a corrente para que irradiem energia irradiada unitária
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
Essa última relação apresenta a capacidade dos modos característicos de diagonalizar o operador de impedância (2) e demonstra a ortogonalidade de campo distante , ou seja,- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.- O espalhamento dinâmico de luz ( DLS ) é uma técnica em física que pode ser usada para determinar o perfil de distribuição de tamanho de pequenas partículas em suspensão ou polímeros em solução . [1] No âmbito do DLS, as flutuações temporais são geralmente analisadas por meio da função de autocorrelação de intensidade ou fóton (também conhecida como espectroscopia de correlação de fótons ou espalhamento de luz quase elástico).) Na análise do domínio do tempo, a função de autocorrelação (ACF) geralmente decai a partir do tempo de atraso zero, e dinâmicas mais rápidas devido a partículas menores levam a uma correlação mais rápida do rastreamento de intensidade dispersa. Foi demonstrado que a intensidade ACF é a transformação de Fourier do espectro de potência e, portanto, as medições de DLS podem ser igualmente bem executadas no domínio espectral. [2] [3] O DLS também pode ser usado para investigar o comportamento de fluidos complexos, como soluções de polímeros concentrados.
Configuração [ editar ]
Uma fonte de luz monocromática, geralmente um laser, é disparada através de um polarizador e em uma amostra. A luz dispersa passa então por um segundo polarizador, onde é coletada por um fotomultiplicador e a imagem resultante é projetada na tela. Isso é conhecido como padrão de manchas (Figura 1). [4]Todas as moléculas na solução estão sendo atingidas pela luz e todas as moléculas difratam a luz em todas as direções. A luz difratada de todas as moléculas pode interferir construtivamente (regiões claras) ou destrutivamente (regiões escuras). Esse processo é repetido em curtos intervalos de tempo e o conjunto resultante de padrões de manchas é analisado por um autocorrelador que compara a intensidade da luz em cada ponto ao longo do tempo. Os polarizadores podem ser configurados em duas configurações geométricas. Uma é uma geometria vertical / vertical (VV), em que o segundo polarizador permite que a luz passe na mesma direção que o polarizador primário. Na geometria vertical / horizontal (VH), o segundo polarizador permite que a luz não esteja na mesma direção da luz incidente.Descrição [ editar ]
Quando a luz atinge pequenas partículas, a luz se espalha em todas as direções ( dispersão de Rayleigh ), desde que as partículas sejam pequenas comparadas ao comprimento de onda (abaixo de 250 nm ). Mesmo que a fonte de luz seja um laser e, portanto, monocromática e coerente , a intensidade da dispersão varia com o tempo. Essa flutuação é devida a pequenas moléculas em soluções submetidas ao movimento brownianoe, portanto, a distância entre os dispersores na solução muda constantemente com o tempo. Essa luz dispersa sofre interferência construtiva ou destrutiva pelas partículas circundantes e, dentro dessa flutuação de intensidade, há informações sobre a escala de tempo do movimento dos dispersores. A preparação da amostra por filtração ou centrifugação é crítica para remover poeira e artefatos da solução.A informação dinâmica das partículas é derivada de uma autocorrelação do traço de intensidade registrado durante o experimento. A curva de autocorrelação de segunda ordem é gerada a partir do rastreamento de intensidade da seguinte maneira:- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde g 2 ( q ; τ ) é a função de autocorrelação em um vetor de onda específico, q , e o tempo de atraso, τ , e I é a intensidade. Os colchetes angulares <> denotam o operador de valor esperado , que em alguns textos é indicado por E maiúsculo .Em curto espaço de tempo, a correlação é alta porque as partículas não têm a chance de se mover em grande parte do estado inicial em que estavam. Os dois sinais são, portanto, essencialmente inalterados quando comparados após apenas um intervalo de tempo muito curto. À medida que os atrasos se tornam mais longos, a correlação decai exponencialmente, o que significa que, após um longo período de tempo, não há correlação entre a intensidade dispersa dos estados inicial e final. Esse decaimento exponencial está relacionado ao movimento das partículas, especificamente ao coeficiente de difusão. Para ajustar o decaimento (isto é, a função de autocorrelação), métodos numéricos são usados, com base nos cálculos das distribuições assumidas. Se a amostra é monodispersaentão a decadência é simplesmente um único exponencial. A equação de Siegert relaciona a função de autocorrelação de segunda ordem com a função de autocorrelação de primeira ordem g 1 ( q ; τ ) da seguinte maneira:- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde o parâmetro β é um fator de correção que depende da geometria e do alinhamento do feixe de laser na configuração da dispersão da luz. É aproximadamente igual ao inverso do número de manchas (consulte Padrão de manchas ) a partir do qual a luz é coletada. Um foco menor do feixe de laser produz um padrão de manchas mais grosseiras, um número menor de manchas no detector e, portanto, uma autocorrelação maior de segunda ordem.O uso mais importante da função de autocorrelação é seu uso na determinação do tamanho.Espalhamento múltiplo [ editar ]
A dispersão dinâmica da luz fornece informações sobre as propriedades dinâmicas de materiais macios, medindo eventos de dispersão únicos, o que significa que cada fóton detectado foi dispersado pela amostra exatamente uma vez. No entanto, a aplicação a muitos sistemas de relevância científica e industrial foi limitada devido à dispersão múltipla frequentemente encontrada, em que os fótons são dispersos várias vezes pela amostra antes de serem detectados. A interpretação precisa se torna extremamente difícil para sistemas com contribuições não negligenciáveis da dispersão múltipla. Especialmente para partículas maiores e com alto índice de refração, isso limita a técnica a concentrações muito baixas de partículas; portanto, uma grande variedade de sistemas é excluída das investigações com espalhamento dinâmico de luz. No entanto, como mostra Schaetzel,[5] é possível suprimir a dispersão múltipla em experimentos de dispersão dinâmica da luz por meio de uma abordagem de correlação cruzada. A idéia geral é isolar a luz dispersa individualmente e suprimir contribuições indesejadas da dispersão múltipla em um experimento de dispersão dinâmica da luz. Diferentes implementações de espalhamento de luz de correlação cruzada foram desenvolvidas e aplicadas. Atualmente, o esquema mais utilizado é o chamado método de espalhamento de luz dinâmico em 3D. [6] [7] O mesmo método também pode ser usado para corrigirdados de espalhamento de luz estática para múltiplas contribuições de espalhamento. [8] Alternativamente, no limite da dispersão múltipla forte, uma variante da dispersão dinâmica da luz chamada espectroscopia de ondas difusas pode ser aplicado.A análise dos dados [ editar ]
Introdução [ editar ]
Depois que os dados de autocorrelação foram gerados, diferentes abordagens matemáticas podem ser empregadas para determinar 'informações' a partir deles. A análise da dispersão é facilitada quando as partículas não interagem através de colisões ou forças eletrostáticas entre os íons. As colisões entre partículas e partículas podem ser suprimidas pela diluição e os efeitos de carga são reduzidos pelo uso de sais para colapsar a dupla camada elétrica .A abordagem mais simples é tratar a função de autocorrelação de primeira ordem como um único decaimento exponencial. Isso é apropriado para uma população monodispersa.- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde Γ é a taxa de decaimento. A difusão de translação coeficiente D t pode ser derivado em um único ângulo ou a uma gama de ângulos, dependendo do vetor de onda q .com- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde λ é o comprimento de onda do laser incidente, n 0 é o índice de refração da amostra e θ é o ângulo no qual o detector está localizado em relação à célula da amostra.Dependendo da anisotropia e polidispersidade do sistema, um gráfico resultante de (Γ / q 2 ) vs. q 2 pode ou não mostrar uma dependência angular. Pequenas partículas esféricas não mostrarão dependência angular e, portanto, nenhuma anisotropia. Um gráfico de (Γ / q 2 ) vs. q 2 resultará em uma linha horizontal. Partículas com uma forma diferente de uma esfera mostrarão anisotropia e, portanto, uma dependência angular ao traçar (Γ / q 2 ) vs. q 2 . [9] A interceptação será, em qualquer caso, o Dt . Portanto, existe um ângulo ótimo de detecção θ para cada tamanho de partícula. Uma análise de alta qualidade deve sempre ser realizada em vários ângulos de dispersão (DLS multiangular). Isso se torna ainda mais importante em uma amostra polidispersa com uma distribuição de tamanho de partícula desconhecida. Em certos ângulos, a intensidade de dispersão de algumas partículas sobrecarrega completamente o sinal fraco de dispersão de outras partículas, tornando-as invisíveis para a análise de dados nesse ângulo. Os instrumentos DLS, que funcionam apenas em um ângulo fixo, só podem fornecer bons resultados para algumas partículas. Assim, a precisão indicada de um instrumento DLS com apenas um ângulo de detecção só é verdadeira para determinadas partículas.D t é frequentemente usado para calcular o raio hidrodinâmico de uma esfera através da equação de Stokes-Einstein . É importante notar que o tamanho determinado pela dispersão dinâmica da luz é o tamanho de uma esfera que se move da mesma maneira que o espalhador. Assim, por exemplo, se o dispersor for um polímero de bobina aleatório, o tamanho determinado não será o mesmo que o raio de rotação determinado pela dispersão estática da luz . Também é útil ressaltar que o tamanho obtido incluirá outras moléculas ou moléculas de solvente que se movem com a partícula. Então, por exemplo, ouro coloidalcom uma camada de surfactante parecerá maior pela dispersão dinâmica da luz (que inclui a camada de surfactante) do que pela microscopia eletrônica de transmissão (que não "vê" a camada devido ao baixo contraste).Na maioria dos casos, as amostras são polidispersas. Assim, a função de autocorrelação é uma soma das decaimentos exponenciais correspondentes a cada uma das espécies da população.- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
É tentador obter dados para g 1 ( q ; τ ) e tentar inverter o acima para extrair G (Γ) . Como G (Γ) é proporcional à dispersão relativa de cada espécie, ele contém informações sobre a distribuição dos tamanhos. No entanto, isso é conhecido como um problema incorreto . Os métodos descritos abaixo (e outros) foram desenvolvidos para extrair o máximo possível de informações úteis de uma função de autocorrelação.Método cumulant [ editar ]
Um dos métodos mais comuns é o método cumulante , [10] [11], a partir do qual, além da soma dos exponenciais acima, mais informações podem ser derivadas sobre a variação do sistema da seguinte maneira:- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
onde Γ é a taxa média de decaimento e μ 2 / Γ 2 é o segundo índice de ordem de polidispersidade (ou uma indicação da variância). Um índice de polidispersidade de terceira ordem também pode ser obtido, mas isso é necessário apenas se as partículas do sistema forem altamente polidispersas. O coeficiente de difusão translacional com média de z D z pode ser derivado em um único ângulo ou em uma faixa de ângulos, dependendo do vetor de onda q .É preciso observar que o método cumulante é válido para τ pequeno e G ( Γ ) suficientemente estreito . [12] Raramente deve-se usar parâmetros além de µ 3 , porque o ajuste excessivo de dados com muitos parâmetros em uma expansão de séries de potência renderizará todos os parâmetros, incluindoe µ 2 , menos preciso. [13] O método cumulante é muito menos afetado pelo ruído experimental do que os métodos abaixo.
CONTIN algoritmo [ editar ]
Um método alternativo para analisar a função de autocorrelação pode ser alcançado por meio de uma transformada inversa de Laplace, conhecida como CONTIN, desenvolvida por Steven Provencher. [14] [15] A análise CONTIN é ideal para sistemas heterodispersos , polidispersos e multimodais que não podem ser resolvidos com o método cumulante. A resolução para separar duas populações diferentes de partículas é aproximadamente um fator de cinco ou mais, e a diferença nas intensidades relativas entre duas populações diferentes deve ser menor que 1: 10-5 .Método de entropia máxima [ editar ]
O método de entropia máxima é um método de análise com grande potencial de desenvolvimento. O método também é usado para a quantificação dos dados de velocidade de sedimentação da ultracentrifugação analítica . O método de entropia máxima envolve uma série de etapas iterativas para minimizar o desvio dos dados ajustados dos dados experimentais e subsequentemente reduzir o χ 2 dos dados ajustados.Dispersão de partículas não esféricas [ editar ]
Se a partícula em questão não for esférica, o movimento rotacional deve ser considerado também porque a dispersão da luz será diferente dependendo da orientação. Segundo Pecora, o movimento browniano rotacional afetará a dispersão quando uma partícula atender a duas condições; eles devem ser opticamente e geometricamente anisotrópicos. [16] As moléculas em forma de bastão atendem a esses requisitos, portanto, um coeficiente de difusão rotacional deve ser considerado além de um coeficiente de difusão translacional. Em sua forma mais sucinta, a equação aparece como- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI.
Onde A / B é a razão dos dois modos de relaxamento (translacional e rotacional), M p contém informações sobre o eixo perpendicular ao eixo central da partícula e M l contém informações sobre o eixo paralelo ao eixo central.Em 2007, Peter R. Lang e sua equipe decidiram usar a dispersão dinâmica da luz para determinar o comprimento das partículas e a proporção de nanorods de ouro curtos. [17] Eles escolheram esse método devido ao fato de não destruir a amostra e ter uma configuração relativamente fácil. Ambos os estados de relaxamento foram observados na geometria VV e os coeficientes de difusão de ambos os movimentos foram usados para calcular as proporções das nanopartículas de ouro.
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
- 1Polarização de ondas eletromagnéticas clássicas
- 2Energia, momento e momento angular de uma onda eletromagnética clássica
- 3Filtros ópticos e cristais
- 4Fótons: A conexão com a mecânica quântica
- 5Veja também
- 6Referências
- 7Leitura adicional
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- A amplitude de probabilidade para duas probabilidades sucessivas é o produto de amplitudes para as possibilidades individuais. Por exemplo, a amplitude para o fóton polarizado x ser polarizado circularmente à direita e para o fóton polarizado circularmente direito passar através da polaroide y é
o produto das amplitudes individuais.
- A amplitude de um processo que pode ocorrer de uma de várias maneiras indistinguíveis é a soma das amplitudes de cada uma das maneiras individuais. Por exemplo, a amplitude total para o fóton x polarizado passar através da polaroide y é a soma das amplitudes para ele passar como fóton polarizado circularmente à direita,
mais a amplitude para passar como um fóton polarizado circularmente à esquerda,
- A probabilidade total do processo ocorrer é o valor absoluto ao quadrado da amplitude total calculada por 1 e 2.
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- x
- FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES E TRANSFORMAÇÕES EM CADEIAS , DECADIMENSIONAL E CATEGORIAL .E DE ESTADOS TRANSICIONAIS GRACELI
- Manipulação orientacional de partículas ou agregados de partículas em pinças ópticas [16]
- Codificação de informações de alta largura de banda na comunicação óptica de espaço livre [17]
- Codificação de informações quânticas de maior dimensão, para possíveis aplicações futuras de criptografia quântica ou computação quântica [18] [19] [20]
- Detecção óptica sensível [21]
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.x[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
,
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
XA polarização do fóton é a descrição mecânica quântica da onda eletromagnética do plano sinusoidal polarizado clássico . Um fóton individual pode ser descrito como tendo polarização circular direita ou esquerda ou uma superposição dos dois. Equivalentemente, um fóton pode ser descrito como tendo polarização linear horizontal ou vertical , ou uma superposição dos dois.A descrição da polarização de fótons contém muitos dos conceitos físicos e grande parte das máquinas matemáticas das descrições quânticas mais envolvidas, como a mecânica quântica de um elétron em um poço em potencial. A polarização é um exemplo de um grau de liberdade qubit , que forma uma base fundamental para a compreensão de fenômenos quânticos mais complicados. Grande parte da maquinaria matemática da mecânica quântica, como vetores de estado , amplitudes de probabilidade , operadores unitários e operadores hermitianos , emergem naturalmente das equações clássicas de Maxwell na descrição. O vetor do estado de polarização quântica para o fóton, por exemplo, é idêntico aoVetor Jones , geralmente usado para descrever a polarização de uma onda clássica . Operadores unitários emergem do requisito clássico de conservação de energia de uma onda clássica que se propaga através de meios sem perdas que alteram o estado de polarização da onda. Operadores hermitianos então seguem para transformações infinitesimais de um estado de polarização clássico.Muitas das implicações da maquinaria matemática são facilmente verificadas experimentalmente. De fato, muitas das experiências podem ser realizadas com dois pares (ou um par quebrado) de óculos de sol polaroid .A conexão com a mecânica quântica é feita através da identificação de um tamanho mínimo de pacote, chamado fóton , para energia no campo eletromagnético. A identificação é baseada nas teorias de Planck e na interpretação dessas teorias por Einstein . O princípio da correspondência permite a identificação do momento e do momento angular (chamado rotação ), bem como da energia, com o fóton.Conteúdo
Polarização de ondas eletromagnéticas clássicas [ editar ]
Artigo principal: Polarização (ondas) Esta seção duplica o escopo de outras seções , especificamente soluções de onda plana sinusoidal da equação de onda eletromagnética . ( Julho de 2014 )
Esta seção duplica o escopo de outras seções , especificamente soluções de onda plana sinusoidal da equação de onda eletromagnética . ( Julho de 2014 )Estados de polarização [ editar ]
Polarização linear [ editar ]
Artigo principal: Polarização linearIsso representa uma onda com fasepolarizado em um ângulo
em relação ao eixo x. Nesse caso, o vetor Jones pode ser escrito
Os vetores de estado para polarização linear em x ou y são casos especiais desse vetor de estado.Se os vetores unitários são definidos de forma queeentão o estado de polarização linearmente polarizada pode ser escrito na "base xy" comoPolarização circular [ editar ]
Artigo principal: Polarização circularSe os ângulos de fasee
diferem exatamente
e a amplitude x é igual à amplitude y da onda é polarizada circularmente . O vetor Jones então se torna
onde o sinal de mais indica polarização circular direita e o sinal de menos indica polarização circular esquerda. No caso de polarização circular, o vetor do campo elétrico de magnitude constante gira no plano xy.Se os vetores unitários são definidos de forma queeentão um estado de polarização arbitrário pode ser escrito na "base RL" comoOndeeNós podemos ver issoPolarização elíptica [ editar ]
Artigo principal: Polarização elípticaO caso geral em que o campo elétrico gira no plano xy e possui magnitude variável é chamado de polarização elíptica . O vetor de estado é dado porVisualização geométrica de um estado de polarização arbitrário [ editar ]
Para entender como é um estado de polarização, pode-se observar a órbita que é feita se o estado de polarização for multiplicado por um fator de fase dee depois interpretar as partes reais de seus componentes como coordenadas x e y, respectivamente. Isso é:
Se apenas a forma traçada e a direção da rotação de ( x ( t ), y ( t )) forem consideradas na interpretação do estado de polarização, ou seja, apenas(em que X ( t ) e Y ( t ) são definidos como acima) e se ele é em geral mais circularmente à direita ou à esquerda de polarização circular (ou seja, se | ip R |> | ip L | , ou vice-versa), pode ser visto que a interpretação física será a mesma, mesmo que o estado seja multiplicado por um fator de fase arbitrário, poise o sentido de rotação permanecerá o mesmo. Em outras palavras, não há diferença física entre dois estados de polarizaçãoe
, entre as quais apenas um fator de fase difere.
Pode-se observar que, para um estado linearmente polarizado, M será uma linha no plano xy, com comprimento 2 e seu meio na origem e cuja inclinação é igual a tan ( θ ) . Para um estado polarizado circularmente, M será um círculo com raio 1 / √ 2 e com o meio na origem.Energia, momento e momento angular de uma onda eletromagnética clássica [ editar ]
Densidade de energia das ondas eletromagnéticas clássicos [ editar ]
Energia de uma onda plana [ editar ]
Artigo principal: Densidade de energiaA energia por unidade de volume nos campos eletromagnéticos clássicos é (unidades cgs) e também a unidade de PlanckPara uma onda plana, isso se tornaonde a energia foi calculada sobre um comprimento de onda da onda.Fração de energia em cada componente [ editar ]
A fração de energia no componente x da onda plana écom uma expressão semelhante para o componente y resultando em.
A fração em ambos os componentes éDensidade de impulso de ondas electromagnéticas clássicos [ editar ]
A densidade do momento é dada pelo vetor de PoyntingPara uma onda plana sinusoidal que viaja na direção z, o momento está na direção z e está relacionado à densidade de energia:A densidade do momento foi calculada sobre um comprimento de onda.Densidade de momento angular das ondas eletromagnéticas clássicos [ editar ]
As ondas eletromagnéticas podem ter momento angular orbital e de rotação . [1] A densidade total de momento angular é [ duvidosa - discuta ]Para uma onda plana sinusoidal que se propaga ao longoeixo, a densidade do momento angular orbital desaparece. A densidade do momento angular do spin está no
direção e é dada por
onde novamente a densidade é calculada sobre um comprimento de onda.Filtros ópticos e cristais [ editar ]
Passagem de uma onda clássica através de um filtro polaroid [ editar ]
Um filtro linear transmite um componente de uma onda plana e absorve o componente perpendicular. Nesse caso, se o filtro estiver polarizado na direção x, a fração de energia que passa pelo filtro éExemplo de conservação de energia: Passagem de uma onda clássica através de um cristal birrefringente [ editar ]
Um cristal birrefringente ideal transforma o estado de polarização de uma onda eletromagnética sem perda de energia das ondas. Os cristais birrefringentes, portanto, fornecem um leito de teste ideal para examinar a transformação conservadora dos estados de polarização. Embora esse tratamento ainda seja puramente clássico, ferramentas quânticas padrão, como operadores unitários e hermitianos, que evoluem o estado no tempo, surgem naturalmente.Estados inicial e final [ editar ]
Um cristal birrefringente é um material que possui um eixo óptico com a propriedade de que a luz possui um índice de refração diferente para a luz polarizada paralela ao eixo do que para a luz polarizada perpendicular ao eixo. A luz polarizada paralela ao eixo é chamada de " raios extraordinários " ou " fótons extraordinários ", enquanto a luz polarizada perpendicular ao eixo é chamada de " raios comuns " ou " fótons comuns ". Se uma onda linearmente polarizada colidir com o cristal, o componente extraordinário da onda emergirá do cristal com uma fase diferente da do componente comum. Na linguagem matemática,em relação ao eixo óptico, o vetor do estado incidente pode ser gravado
e o vetor de estado para a onda emergente pode ser escritoEnquanto o estado inicial foi polarizado linearmente, o estado final é elipticamente polarizado. O cristal birrefringente altera o caráter da polarização.Dupla do estado final [ editar ]
O estado inicial de polarização é transformado no estado final com o operador U. A dupla do estado final é dada porOperadores unitários e conservação de energia [ editar ]
A fração de energia que emerge do cristal éNesse caso ideal, toda a energia que entra no cristal emerge do cristal. Um operador U com a propriedade queonde eu sou o operador de identidade e U é chamado de operador unitário . A propriedade unitária é necessária para garantir a conservação de energia nas transformações do estado.Operadores hermitianas e conservação de energia [ editar ]
 Duplamente refratando Calcite da reivindicação Iceberg, Dixon, Novo México. Esse cristal de 16 kg, exposto no Museu Nacional de História Natural , é um dos maiores cristais individuais dos Estados Unidos.Se o cristal for muito fino, o estado final será apenas ligeiramente diferente do estado inicial. O operador unitário estará perto do operador de identidade. Podemos definir o operador H,e o adjunto porA conservação de energia requer entãoIsso requer queA transição infinitesimal do estado de polarização éAssim, a conservação de energia requer que transformações infinitesimais de um estado de polarização ocorram através da ação de um operador hermitiano.
Duplamente refratando Calcite da reivindicação Iceberg, Dixon, Novo México. Esse cristal de 16 kg, exposto no Museu Nacional de História Natural , é um dos maiores cristais individuais dos Estados Unidos.Se o cristal for muito fino, o estado final será apenas ligeiramente diferente do estado inicial. O operador unitário estará perto do operador de identidade. Podemos definir o operador H,e o adjunto porA conservação de energia requer entãoIsso requer queA transição infinitesimal do estado de polarização éAssim, a conservação de energia requer que transformações infinitesimais de um estado de polarização ocorram através da ação de um operador hermitiano.Fótons: A conexão com a mecânica quântica [ editar ]
Artigo principal: PhotonEnergia, momento e momento angular de fótons [ editar ]
Energia [ editar ]
O tratamento até este ponto tem sido clássico . É um testemunho, no entanto, da generalidade das equações de Maxwell para a eletrodinâmica de que o tratamento pode ser tornado mecânico quântico com apenas uma reinterpretação das quantidades clássicas. A reinterpretação é baseada nas teorias de Max Planck e na interpretação de Albert Einstein dessas teorias e de outros experimentos.A conclusão de Einstein de experimentos iniciais sobre o efeito fotoelétrico é que a radiação eletromagnética é composta por pacotes irredutíveis de energia, conhecidos como fótons . A energia de cada pacote está relacionada à frequência angular da onda pela relaçãoOndeé uma quantidade determinada experimentalmente conhecida como constante de Planck . Se houver
fótons em uma caixa de volume
, a energia no campo eletromagnético é
e a densidade de energia éA energia do fóton pode ser relacionada aos campos clássicos através do princípio da correspondência que afirma que, para um grande número de fótons, os tratamentos quântico e clássico devem concordar. Assim, para grandes, a densidade de energia quântica deve ser a mesma que a densidade de energia clássica
O número de fótons na caixa é entãoMomento [ editar ]
O princípio da correspondência também determina o momento e o momento angular do fóton. Para impulsoonde kz é o número da onda. Isso implica que o momento de um fóton éMomento angular e rotação [ editar ]
Da mesma forma para o momento angular do spinonde Ec é a força do campo. Isso implica que o momento angular de rotação do fóton éa interpretação quântica dessa expressão é que o fóton tem uma probabilidade dede ter um momento angular de rotação de
e uma probabilidade de
de ter um momento angular de rotação de
. Podemos, portanto, pensar no momento angular de rotação do fóton sendo quantizado e também na energia. O momento angular da luz clássica foi verificado. [2] Um fóton que é linearmente polarizado (plano polarizado) está em uma superposição de quantidades iguais dos estados canhoto e destro.
Operador de spin [ editar ]
A rotação do fóton é definida como o coeficiente deno cálculo do momento angular do spin. Um fóton possui o spin 1 se estiver no
estado e -1 se estiver no
Estado. O operador de rotação é definido como o produto externo
O valor esperado de uma medição de rotação em um fóton é entãoUm operador S foi associado a uma quantidade observável, o momento angular do spin. Os valores próprios do operador são os valores observáveis permitidos. Isso foi demonstrado para o momento angular do spin, mas geralmente é verdade para qualquer quantidade observável.Estados de spin [ editar ]
Veja também: Polarização circular § Mecânica quânticaPodemos escrever os estados polarizados circularmente comoonde s = 1 paraes = -1 para
. Um estado arbitrário pode ser escrito
Ondee
são ângulos de fase, θ é o ângulo pelo qual o quadro de referência é girado e
Operadores de rotação e momento angular de forma diferencial [ editar ]
Quando o estado é escrito em notação de rotação, o operador de rotação pode ser escritoOs autovetores do operador de rotação diferencial sãoPara ver esta notaO operador de momento angular de rotação éA natureza da probabilidade na mecânica quântica [ editar ]
Probabilidade de um único fóton [ editar ]
Existem duas maneiras pelas quais a probabilidade pode ser aplicada ao comportamento dos fótons; a probabilidade pode ser usada para calcular o número provável de fótons em um estado particular, ou a probabilidade pode ser usada para calcular a probabilidade de um único fóton estar em um estado particular. A primeira interpretação viola a conservação de energia [ citação necessário ] . A última interpretação é a opção viável, se não intuitiva. Dirac explica isso no contexto do experimento de fenda dupla :Algum tempo antes da descoberta da mecânica quântica, as pessoas perceberam que a conexão entre ondas de luz e fótons deve ser de caráter estatístico. O que eles não perceberam claramente, no entanto, foi que a função de onda fornece informações sobre a probabilidade de um fóton estar em um determinado local e não o número provável de fótons naquele local [ duvidoso - discutir ]. A importância da distinção pode ser esclarecida da seguinte maneira. Suponha que tenhamos um feixe de luz que consiste em um grande número de fótons divididos em dois componentes de igual intensidade. Partindo do pressuposto de que o feixe está conectado com o número provável de fótons, devemos ter metade do número total entrando em cada componente. Se os dois componentes agora são feitos para interferir, devemos exigir que um fóton em um componente seja capaz de interferir um no outro. Às vezes, esses dois fótons teriam que se aniquilar e outras vezes teriam que produzir quatro fótons. Isso contradiz a conservação de energia. A nova teoria, que conecta a função de onda com as probabilidades de um fóton, supera a dificuldade, fazendo com que cada fóton entre parcialmente em cada um dos dois componentes. Cada fóton interfere apenas consigo mesmo. A interferência entre dois fótons diferentes nunca ocorre[ duvidoso - discuta ] .
- Paul Dirac, Os princípios da mecânica quântica, quarta edição, capítulo 1Amplitudes de probabilidade [ editar ]
A probabilidade de um fóton estar em um estado de polarização específico depende dos campos calculados pelas equações clássicas de Maxwell. O estado de polarização do fóton é proporcional ao campo. A probabilidade em si é quadrática nos campos e, consequentemente, também é quadrática no estado quântico de polarização. Na mecânica quântica, portanto, o estado ou amplitude de probabilidade contém as informações básicas de probabilidade. Em geral, as regras para combinar amplitudes de probabilidade se parecem muito com as regras clássicas para composição de probabilidades: [A seguinte citação é de Baym, capítulo 1] [ esclarecimentos necessários ]Princípio da incerteza [ editar ]
Artigo principal: Princípio da incertezaPreparação matemática [ editar ]
Para qualquer operador legal [ necessário esclarecimento ] , a desigualdade a seguir, uma conseqüência da desigualdade de Cauchy-Schwarz , é verdadeira.Se BA AB e AB ψ são definidos, subtraindo os meios e reinserindo na fórmula acima, deduzimosOndeAquiEste é um resultado puramente matemático. Nenhuma referência foi feita a qualquer quantidade ou princípio físico. Simplesmente afirma que a incerteza de um operador vezes a incerteza de outro operador tem um limite inferior.Aplicação ao momento angular [ editar ]
A conexão com a física pode ser feita se identificarmos os operadores com operadores físicos, como o momento angular e o ângulo de polarização. Nós temos entãoo que significa que o momento angular e o ângulo de polarização não podem ser medidos simultaneamente com precisão infinita. (O ângulo de polarização pode ser medido verificando se o fóton pode passar por um filtro polarizador orientado em um ângulo específico ou por um divisor de feixe de polarização . Isso resulta em uma resposta sim / não que, se o fóton foi polarizado no plano em algum outro ângulo, depende da diferença entre os dois ângulos.)Estados, amplitudes de probabilidade, operadores unitários e hermitianos e vetores próprios [ editar ]
Grande parte do aparato matemático da mecânica quântica aparece na descrição clássica de uma onda eletromagnética sinusoidal polarizada. O vetor Jones para uma onda clássica, por exemplo, é idêntico ao vetor do estado de polarização quântica para um fóton. Os componentes circulares direito e esquerdo do vetor Jones podem ser interpretados como amplitudes de probabilidade dos estados de rotação do fóton. A conservação de energia requer que os estados sejam transformados com uma operação unitária. Isso implica que transformações infinitesimais são transformadas com um operador hermitiano. Essas conclusões são uma conseqüência natural da estrutura das equações de Maxwell para ondas clássicas.A mecânica quântica entra em cena quando as quantidades observadas são medidas e consideradas discretas, e não contínuas. Os valores observáveis permitidos são determinados pelos valores próprios dos operadores associados ao observável. No momento angular do caso, por exemplo, os valores observáveis permitidos são os autovalores do operador de rotação.Esses conceitos emergiram naturalmente das equações de Maxwell e das teorias de Planck e Einstein. Eles foram encontrados para ser verdade em muitos outros sistemas físicos. De fato, o programa típico é assumir os conceitos desta seção e, em seguida, inferir a dinâmica desconhecida de um sistema físico. Isso foi feito, por exemplo, com a dinâmica dos elétrons. Nesse caso, partindo dos princípios desta seção, a dinâmica quântica de partículas foi inferida, levando à equação de Schrödinger , um afastamento da mecânica newtoniana . A solução desta equação para átomos levou à explicação da série Balmer para espectros atômicos e, consequentemente, formou uma base para toda a física e química atômicas.Esta não é a única ocasião [ duvidosa - discutir ] em que as equações de Maxwell ter forçado uma reestruturação da mecânica newtoniana. As equações de Maxwell são relativisticamente consistentes. A relatividade especial resultou de tentativas de tornar a mecânica clássica consistente com as equações de Maxwell (veja, por exemplo, Problema com ímã em movimento e condutor ).O momento angular da luz é uma quantidade vetorial que expressa a quantidade de rotação dinâmica presente no campo eletromagnético da luz . Enquanto viaja aproximadamente em linha recta, um feixe de luz também pode ser rotativo (ou “ fiação ”, ou “ torção ”) em torno do seu próprio eixo. Essa rotação, embora não seja visível a olho nu , pode ser revelada pela interação do feixe de luz com a matéria.Existem duas formas distintas de rotação de um feixe de luz, uma envolvendo sua polarização e a outra sua forma de frente de onda . Portanto, essas duas formas de rotação estão associadas a duas formas distintas de momento angular , respectivamente denominadas momento angular de rotação da luz (SAM) e momento angular da órbita leve (OAM).O momento angular total da luz (ou, mais geralmente, do campo eletromagnético e dos outros campos de força ) e da matéria é conservado no tempo.Introdução [ editar ]
É sabido que a luz, ou mais geralmente uma onda eletromagnética , transporta não apenas energia, mas também momento , que é uma propriedade característica de todos os objetos em movimento translacional . A existência desse momento se torna aparente no fenômeno “ pressão de radiação ”, no qual um feixe de luz transfere seu momento para um objeto absorvente ou dispersante, gerando uma pressão mecânica sobre ele no processo.Menos conhecido é o fato de que a luz também pode carregar momento angular , que é uma propriedade de todos os objetos em movimento rotacional. Por exemplo, um feixe de luz pode girar em torno de seu próprio eixo enquanto se propaga para a frente. Novamente, a existência desse momento angular pode ser evidenciada transferindo-o para pequenas partículas absorventes ou dispersantes, que são, portanto, sujeitas a um torque óptico.Para um feixe de luz, geralmente é possível distinguir duas " formas de rotação ", a primeira associada à rotação dinâmica dos campos elétrico e magnético ao redor da direção de propagação e a segunda à rotação dinâmica dos raios de luz em torno do eixo principal do feixe. Essas duas rotações estão associadas a duas formas de momento angular , a saber, SAM e OAM. No entanto, essa distinção fica embaçada para feixes fortemente focados ou divergentes e, no caso geral, apenas o momento angular total de um campo de luz pode ser definido. Um caso limitante importante em que a distinção é clara e inequívoca é o de um feixe de luz “ paraxial ”, que é bem colimadofeixe no qual todos os raios de luz (ou, mais precisamente, todos os componentes de Fourier do campo óptico ) formam apenas pequenos ângulos com o eixo do feixe .Para esse feixe, o SAM está estritamente relacionado à polarização óptica e, em particular, à chamada polarização circular . OAM está relacionado à distribuição do campo espacial e, em particular, à forma helicoidal da frente de onda .Além desses dois termos, se a origem das coordenadas estiver localizada fora do eixo da viga, haverá uma terceira contribuição do momento angular obtida como produto cruzado da posição da viga e seu momento total . Este terceiro termo também é chamado de " orbital ", porque depende da distribuição espacial do campo. No entanto, como seu valor depende da escolha da origem, é denominado momento angular orbital “ externo ” , em oposição ao OAM “ interno ” que aparece para os feixes helicoidais.Expressões matemáticas para o momento angular da luz [ editar ]
Uma expressão comumente usada para o momento angular total de um campo eletromagnético é a seguinte, na qual não há distinção explícita entre as duas formas de rotação:Ondee
são os campos elétrico e magnético, respectivamente,
é a permissividade do vácuo e estamos usando unidades SI.
No entanto, outra expressão do momento angular que surge naturalmente do teorema de Noether é a seguinte, na qual existem dois termos separados que podem estar associados ao SAM () e OAM (
): [1]
Ondeé o potencial vetorial do campo magnético e os símbolos sobrescritos em i denotam os componentes cartesianos dos vetores correspondentes.
Pode-se provar que essas duas expressões são equivalentes entre si para qualquer campo eletromagnético que desaparece rápido o suficiente fora de uma região finita do espaço. Os dois termos na segunda expressão, porém, são fisicamente ambíguo, como eles não são de calibre - invariante . Uma versão invariável do medidor pode ser obtida substituindo o potencial vetorial A e o campo elétrico E pelo seu componente "transversal" ou radiativoe
, obtendo assim a seguinte expressão:
Uma justificativa para dar esse passo ainda está para ser fornecida. A última expressão tem outros problemas, pois pode ser demonstrado que os dois termos não são verdadeiros momentos angulares, pois não obedecem às regras corretas de comutação quântica. A soma deles, que é o momento angular total, é o que acontece. [ citação necessária ]Uma expressão equivalente, porém mais simples, para uma onda monocromática de frequência ω, usando a notação complexa para os campos, é a seguinte: [2]Vamos agora considerar o limite paraxial, assumindo que o eixo do feixe coincide com o eixo z do sistema de coordenadas. Nesse limite, o único componente significativo do momento angular é o z, que é o momento angular que mede a rotação do feixe de luz em torno de seu próprio eixo, enquanto os outros dois componentes são desprezíveis.Ondee
denotam os componentes de polarização circular esquerda e direita, respectivamente.
Troca de rotação e momento angular orbital com a matéria [ editar ]
Quando um feixe de luz com momento angular diferente de zero colide com uma partícula absorvente, seu momento angular pode ser transferido para a partícula, configurando-a em movimento rotacional. Isso ocorre com o SAM e o OAM. No entanto, se a partícula não estiver no centro do feixe, os dois momentos angulares darão origem a diferentes tipos de rotação da partícula. O SAM dará origem a uma rotação da partícula em torno de seu próprio centro, ou seja, a uma rotação da partícula. OAM, em vez disso, irá gerar uma revolução da partícula em torno do eixo do feixe. [3] [4] [5] Esses fenômenos são esquematicamente ilustrados na figura.No caso de meios transparentes, no limite paraxial, o SAM óptico é trocado principalmente por sistemas anisotrópicos, por exemplo cristais birrefringentes . De fato, placas finas de cristais birrefringentes são comumente usadas para manipular a polarização da luz. Sempre que a elipticidade da polarização é alterada, no processo, ocorre uma troca de SAM entre a luz e o cristal. Se o cristal estiver livre para girar, ele fará isso. Caso contrário, o SAM é finalmente transferido para o titular e para a Terra.Placa de fase espiral (SPP) [ editar ]
No limite paraxial, o OAM de um feixe de luz pode ser trocado por meios materiais que possuem uma heterogeneidade espacial transversal. Por exemplo, um feixe de luz pode adquirir OAM cruzando uma placa de fase espiral, com uma espessura não homogênea (veja a figura). [6]Holograma de forquilha [ editar ]
Uma abordagem mais conveniente para gerar OAM baseia-se no uso da difração em um holograma semelhante a um garfo ou forcado (veja a figura). [7] [8] [9] [10] Os hologramas também podem ser gerados dinamicamente sob o controle de um computador usando um modulador espacial de luz . [11]Q-Plate [ editar ]
Outro método para gerar OAM é baseado no acoplamento SAM-OAM que pode ocorrer em um meio que é anisotrópico e não homogêneo. Em particular, a chamada placa q é um dispositivo, atualmente realizado usando cristais líquidos, polímeros ou redes de sub comprimentos de onda, que podem gerar OAM explorando uma alteração de sinal SAM. Nesse caso, o sinal OAM é controlado pela polarização de entrada. [12] [13] [14]Conversores de modo cilíndrico [ editar ]
OAM também pode ser gerado convertendo um feixe Hermite-Gaussiano em um feixe Laguerre-Gaussiano usando um sistema astigmático com duas lentes cilíndricas bem alinhadas colocadas a uma distância específica (veja a figura) para introduzir uma fase relativa bem definida entre vigas Hermite-Gaussianas horizontais e verticais. [15]Possíveis aplicações do momento angular orbital da luz [ editar ]
As aplicações do momento angular de rotação da luz são indistinguíveis das inúmeras aplicações da polarização da luz e não serão discutidas aqui. As possíveis aplicações do momento angular orbital da luz são atualmente objeto de pesquisa. Em particular, as seguintes aplicações já foram demonstradas em laboratórios de pesquisa, embora ainda não tenham atingido o estágio de comercialização:Assinar: Postagens (Atom)
Assinar: Postagens (Atom)
Postado por cientista, teólogo, filósofo, pintor, compositor Ancelmo Luiz Graceli às 01:53 Nenhum comentário:
Assinar: Postagens (Atom)
- Gerar link
- X
- Outros aplicativos
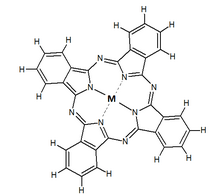





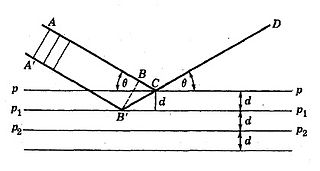






























![{\ displaystyle \ mathbf {Z} = \ mathbf {R} + \ mathrm {j} \ mathbf {X} = \ left [Z_ {uv} \ right] = \ left [\, \ int \ limits _ {\ Omega } {\ boldsymbol {\ psi}} _ {u} ^ {\ ast} \ cdot {\ mathcal {Z}} \ left ({\ boldsymbol {\ psi}} _ {v} \ right) \, \ mathrm { d} S \ direita].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/758f4f7e1ad476e667bda2b4e2c360a4d55e674a)










![g ^ {2} (q; \ tau) = 1 + \ beta \ left [g ^ {1} (q; \ tau) \ right] ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec3b1e787d6c8072a7b9291b748854e4899c7ab1)






















![\ begin {pmatrix} x (t) \\ y (t) \ end {pmatrix} = \ begin {pmatrix} \ Re (e ^ {i \ omega t} \ psi_x) \\ \ Re (e ^ {i \ omega t} \ psi_y) \ end {pmatrix} = \ Re \ left [e ^ {i \ omega t} \ begin {pmatrix} \ psi_x \\ \ psi_y \ end {pmatrix} \ right] = \ Re \ left ( e ^ {i \ omega t} | \ psi \ rangle \ right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/36cad9147abe815aca88d1a6c1b7454f60b00259)


![\ mathcal {E} _c = \ frac {1} {8 \ pi} \ left [\ mathbf {E} ^ 2 (\ mathbf {r}, t) + \ mathbf {B} ^ 2 (\ mathbf {r} , t) \ direita].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4cfdb305a8a57cf2e0eb86eb8454e66a874240e)





![\ boldsymbol {\ mathcal {L}} = \ mathbf {r} \ times \ boldsymbol {\ mathcal {P}} = {1 \ over 4 \ pi c} \ mathbf {r} \ times \ left [\ mathbf {E } (\ mathbf {r}, t) \ times \ mathbf {B} (\ mathbf {r}, t) \ direita].](https://wikimedia.org/api/rest_v1/media/math/render/svg/958c7b1b6c990fc7aca959791d1916ab5f1c2e78)
































![\ hat {S} _d \ exp \ left (i \ alpha_x -é \ theta \ right) | s \ rangle \ rightarrow i {\ parcial \ over \ parcial \ theta} \ exp \ left (i \ alpha_x -is \ theta \ right) | s \ rangle = s \ left [\ exp \ left (i \ alpha_x -é \ theta \ right) | s \ rangle \ right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/58670d802101d4dbf2b8c88bad98e92fde6fa3c7)






![\ Delta _ {\ psi} \ hat {A} \, \ Delta _ {\ psi} \ hat {B} \ ge \ frac {1} {2} \ left | \ left \ langle \ left [{\ hat {A} }, {\ hat {B}} \ right] \ right \ rangle_ \ psi \ right |](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d15ab2a4d2c0b105f736f14dc02fcf35234c952)


![\ left [{\ hat {A}}, {\ hat {B}} \ right] \ \ stackrel {\ mathrm {def}} {=} \ \ hat {A} \ hat {B} - \ hat {B } \ hat {A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abfbb15ab65096d66623a01567abd271a0745631)










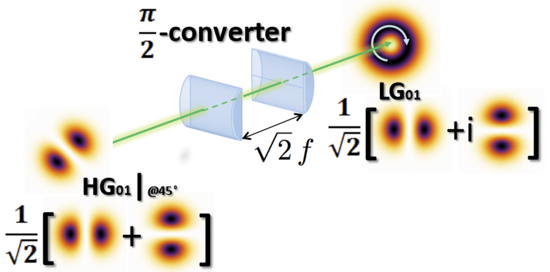
Comentários
Postar um comentário